Пусть матрица Х коэффициентов уравнений наблюдений (6) имеет полный ранг, а случайные возмущения (8) удовлетворяют четырем условиям:
E(ε1) = E(ε2) = … = E(εn) = 0, (15)
Var(ε1) = Var(ε2) = … = Var(εn) = σ2(16)
Cov(εi, εj) = 0 при i≠j(17)
Cov(xi,εj) = 0 при всех значениях i и j (18)
В этом случае справедливы следующие утверждения:
а) наилучшая линейная процедура (13), приводящая к несмещенной и эффективной оценке (11), имеет вид:
![]()
б) линейная несмещенная эффективная оценка (19) обладает свойством наименьших квадратов:
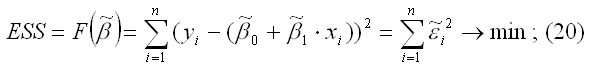
в) ковариационная матрица оценки (19) вычисляется по правилу:
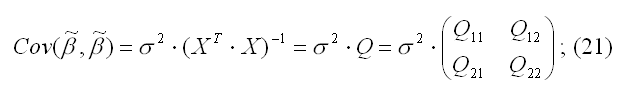
г) несмещенная оценка параметра σ2 модели (2) находится по формуле:
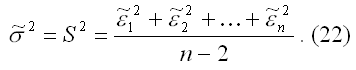
Следствие теоремы Гаусса-Маркова. Оценка
![]()
доставляемая процедурой (19) метода наименьших квадратов, может быть вычислена в процессе решения системы двух линейных алгебраических уравнений:
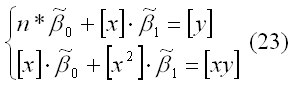
Данная система называется системой нормальных уравнений. Ее коэффициенты и свободные члены определяются по правилам:
= x1 + x2 +…+ xn,
= y1 + y2 +…+ yn, (24)
x2] = x12 + x22 +…+ xn2,
= x1*y1 + x2*y2 + … + xn*yn.
Явный вид решения системы (23):
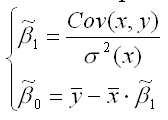
Поможем написать любую работу на аналогичную тему

