Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b = 0, и следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от средне го значения у на две части - «объясненную» и «необъясненную»:
- общая сумма квадратов отклонений
- сумма квадратов отклонения объясненная регрессией 
- остаточная сумма квадратов отклонения.
|
|
Любая сумма квадратов отклонений связана с числом степеней свободы, т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности nис числом определяемых по ней констант. Применительно к исследуемой проблеме число cтепеней свободы должно показать, сколько независимых отклонений из п возможных требуется для образования данной суммы квадратов.
Дисперсия на одну степень свободы D.
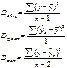
F-отношения (F-критерий): 
Ecли нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Н0 необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным, если о больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл Н0 отклоняется.
Если же величина окажется меньше табличной Fфакт ‹, Fтабл , то вероятность нулевой гипотезы выше заданного уровня и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется.
Стандартная ошибка коэффициента регрессии
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдентa: 
которое
затем сравнивается с табличным значением при определенном уровне значимости 
и числе степеней свободы (n- 2).
Стандартная ошибка параметра а:
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции тr:
Общая дисперсия признака х: 
Коэф. регрессии 
Его величина показывает ср. изменение результата с изменением фактора на 1 ед.
Ошибка аппроксимации: 
Поможем написать любую работу на аналогичную тему