Оценка сущности параметров линейной регрессии и корреляции.

После нахождения уравнения линейной регрессии  проводится оценка значимости как уравнения в целом, так и его параметров. Оценка значимости уравнения регрессии в целом производится при помощи критерия Фишера. В основе лежит гипотеза о том, что коэффициент регрессии b=0, откуда фактор х не оказывает никакого влияния на результативный  признак y. До начала расчета F- критерия производится анализ дисперсии. В основе этого анализа лежит правило сложной дисперсии.

Общая сумма квадратов отклонений индивидуальных значений результативного признака y от среднего значения  вызывается влиянием множества причин. Эти причины можно разделит на две группы.

1. Изучаемый фактор х.

2. Все другие факторы.

Если фактор х не оказывает влияния на результат, то линия регрессии на графике параллельна оси Ох и среднее значение y равно расчетному:  Тогда все дисперсии результативного признака обусловлены воздействием прочих факторов и общая сумма квадратов отклонений совпадает с остаточной.

Если прочие факторы не влияют на результат, то связь х и y функциональна, а остаток суммы квадратов равен нулю. Сумма квадратов объясненных регрессий в этом случае совпадает с общей суммой квадратов.

В связи с тем, что не все точки поля корреляции лежат на линии регрессии имеет место разброс, обусловленный как влиянием фактора х, т.е. регрессией, так и вызванный действием прочих причин (необъясненные возмущения). В зависимости от того, какая часть объединенной вариации признака y приходится на объясняющую вариацию, делают вывод о том, пригодна ли линейная регрессия для прогноза. Если сумма квадратов отклонений, обусловленная регрессией будет больше остаточной суммы квадратов, то уравнение регрессии считается статистически значимым, а фактор х оказывает существенное воздействие на результативный признак y. В таком случае коэффициент детерминации r2 будет приближаться к единице.

Любая сумма квадратов отклонений  связана с числом степеней свободы, т.е. с числом свободы, независимого варьирования признака. Его значение связано с числом единиц совокупности n и с числом определяемых постоянных m (а, b). Для объединенной суммы квадратов число степеней свобода равно n-1. Объясненная или функциональная сумма квадратов имеет одну степень свободы, т.е. равна единице. Существует равенство между числом степеней свободы  общей факторной и остаточной сумме квадратов, потому что степеней свободы для остаточной суммы квадратов равно n-2. При делении каждый из суммы квадратов на соответствующее число степеней свободы получают среднее квадратическое отклонение и дисперсию: σ2 – общее, σ2 – объясненная и σ2 – остаточная.

Сопоставляя фактическую и остаточную дисперсии в расчете на одну степень свободы, получаем F – отношение или F- критерий

Если нулевая гипотеза справедлива, то фактическая и остаточная дисперсии не отличаются друг от друга. Для нулевой гипотезы необходимо опровержение, чтобы фактор дисперсии превышал остаток  в несколько раз. Разработаны специальные таблицы критических значений F- критерия при разных уровнях сущности нулевой гипотезы и различным числом степеней свободы. Табличное значение F – критерия это максимальная величина отклонения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F – отклонения признается достоверным (отличающимся от границы), если оно больше таблиц. В этом случае нулевая гипотеза об отсутствии связи отклоняется и дается вывод о сущности этой связи Fфакт. > Fтабл.. Если Fфакт. < Fтабл., то вероятность нулевой гипотезы выше данного уровня и она не может быть отклонена без риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически не значимы, нулевая гипотеза не отклоняется. Оценка значимости уравнения регрессии обычно делается в виде таблицы.

Дисперсионный анализ результатов регрессии.

Кроме того оцениваются и отдельные параметры уравнения регрессии. Определяется стандартные ошибки по каждому из множеств.

Стандартная ошибка коэффициента регрессии

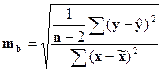
Стандартная ошибка влияет вместе с t – распределением Стьюдента применяется для проверки сущности коэффициента регрессии и для расчетов по завершению интервалов. Для оценки сущности коэффициента регрессии по величине  сравниваются по стандартным ошибкам, т.е. определяется фактическое значение t- критерия Стьюдента

,

которая затем сравнивается с табличным значением при определенном уровне значимости α и в числе степеней свободы n-1. Связь между F – критерием Фишера и t – статистикой Стьюдента, имеет вид

Если фактическое значение F – критерия превышает табличное, то гипотезу о сущности коэффициента регрессии можно отклонить, а доверительный интервал для коэффициента регрессии определить как

b ± t mb

В связи с тем, что коэффициент регрессии в экономических исследованиях имеет четкую интерпретацию, доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов. Например. Интервал -10≤ b ≤ 40. Такая запись одновременно содержит и положительные и отрицательные величины и даже 0, это не может быть.

Стандартная ошибка параметра а определяется по формуле:

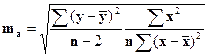
Процедура оценивания сущности параметра а не отличается от рассмотренной оценки коэффициента регрессии b.

Его величина сравнивается с табличным значением при степени свободы (n-2).

Значимость минимального коэффициента корреляции

Фактическое значение F – критерия Стьюдента определяется как

Связь F – критерия с t – статистикой Стьюдента

Если tтабл < tфакт, то нулевая гипотеза отклоняется, т.е. а, b,r – не случайно отличаются от нуля и сформировались под влиянием сис – ки действительного фактора а.

Если tтабл > tфакт, то нулевая гипотеза не отклоняется и признается случайная природа формирования а, b,r.