Оценка значимости уравнения регрессии в целом дается с помощью критерия Фишера. Перед расчетом критерия проводится дисперсионный анализ.
Общая сумма квадратов отклонений у от его среднего значения раскладывается на объясненную и остаточную регрессии:
общая объяснен остаточная
Если фактор не оказывает влияние на результат, то теоретические значения будут равны среднему.
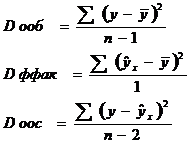Разделив суммы квадратов на соответствующее число степеней свободы, получили дисперсии:
Расчетное значение критерия Фишера находится по формуле: 
Fтабл. определяется по таблицам распределения Фишера с учетом уровня значимости ά=0,05/0,01/0,1 и числом степеней свободы ν1 = 1, ν2=n-2. Если Фрасч>Фтабл, уравнение регрессии признается значимым.
Значимость уравнения множественной регрессии оценивается с помощью Ф-критерия Фишера:
M – число параметров при х
Фтабл при α=0,05 V1=m V2=n-m-1
Факт>Фтабл уравнение значимо.
Можно оценить значимость не только уравнения в целом, но и фактора дополнительно включенного в модель. Для этого определяется частный Ф критерий. Оценим значимость влияния х1 как дополнительно включенного фактора:
R2yx1x2xn – коэффициент множественной детерминации для модели с полным набором факторов
R2yx2x3xn - коэффициент множественной детерминации для модели без учета Х1
Фх1 сравнивается с Фтабл при α=0,05 V1=1 V2=n-m-1
Фх1>Фтабл – дополнительное включение фактора Х1 в модель статистики оправдано и коэффициент чистой регрессии b1 статистики значим.
Фх1<Фтабл – фактор Х1 нецелесообразно включать в модель и коэффициент чистой регрессии статистики незначим
Поможем написать любую работу на аналогичную тему