Значимость уравнения множественной регрессии в целом может оцениваться не только с помощью F-критерия Фишера, но также и с применением дисперсионного анализа.
Пример. Предположим, что модель урожайности пшеницы y (ц/га) от количества внесенных минеральных удобрений на 1га x1 и осадков x2 (мм) характеризуется следующим уравнением:
При этом 
Результаты дисперсионного анализа оказываются следующими:
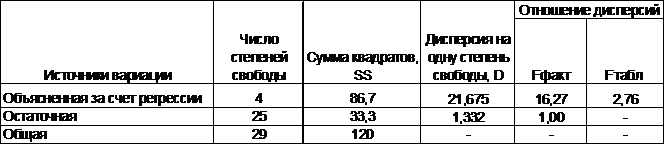
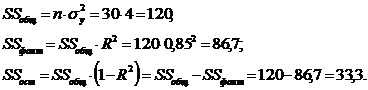
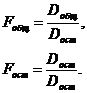
При расчете частных F-критериев также применяется дисперсионный анализ.
Пример. Применим частный F-критерий для оценки значимости коэффициентов регрессии в уравнении множественной регрессии, описывающей зависимость объема продукции y от затрат труда x1 и технической оснащенности производства x2:
В рассматриваемом примере 
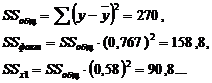Вычисления аналогично.
В таблице приведены три значения F-критерия. В первой строке указан общий F-критерий. Он составил 19,3 и характеризует значимость двухфакторного уравнения регрессии в целом. Вторая величина F=22,0 характеризует значимость парной регрессии 
при условии, что остаточная дисперсия совпадает с величиной остаточной дисперсии для множественной регрессии. Третье значение F=16,5 – это частный F-критерий, оценивающий значимость дополнительного включения в модель фактора 
после введения в нее фактора 
Эта таблица отличается от таблиц результатов дисперсионного анализа, рассматриваемых ранее. В ней источник вариации «регрессия» раскладывается на две составляющие:
1) обусловленная влиянием фактора x1 ;
2) обусловленная дополнительным включением в регрессионную модель фактора x2.
Чтобы получить частный F-критерий для фактора x1 необходимо построить другую таблицу.
Поможем написать любую работу на аналогичную тему