Спецификация модели для парной регрессии (возмущение, способы выбора вида математической функции).

Спецификация модели – подробное описание поведения объекта на математическом языке

В эконометрике широко используются методы статистики. Ставя цель дать количественное описание взаимосвязей между экономическими  переменными, эконометрика прежде всего связана с методами регрессии и корреляции.

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессию.

Простая регрессия представляет собой регрессию между двумя переменными – y и x, т.е. модель вида

, где  y – зависимая переменная (результативный признак)

                        x – независимая, или объясняющая, переменная (признак-фактор).

Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т.е. модель вида

Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными словами, исследование начинается с теории, устанавливающей связь между явлениями.

Прежде всего, из круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который используется в качестве объясняющей переменной. Предположим, что выдвигается гипотеза о том, что величина спроса y на товар A находится в обратной  зависимости от цены x, т.е. . В этом случае необходимо знать, какие остальные факторы предполагаются неизменными, возможно, в дальнейшем их придется учесть в модели и от простой регрессии перейти к множественной.

Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина y складывается из двух слагаемых:

, где yi – фактическое значение результативного признака

yxi – теоретическое значение результативного признака, найденной исходя из соответствующей математической функции связи y и x, т.е. из уравнения регрессии

ei – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии

Случайная величина e также называется возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенности измерения. Ее присутствие в модели порождено тремя источниками:

- спецификация модели

- выборочный характер исходных данных

- особенности измерения переменных.

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретическое значение результативного признака  подходят к фактическим данным y.

К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для , но и недоучет в уравнении регрессии какого-либо существенного фактора, т.е. использование парной регрессии вместо множественной.

Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки могут иметь место в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.

Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии.

Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшит, изменяя форму модели, а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при исследовании на макроуровне.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.

В парной регрессии выбор вида математической функции  может быть осуществлен тремя методами:

- графическим

- аналитическим, т.е. исходя из теории изучаемой взаимосвязи

- экспериментальным

При изучении зависимости между двумя признаками графический метод подбора уравнения регрессии достаточно нагляден. Он основан на поле корреляции.

Основные типы кривых, используемых при количественной оценке:

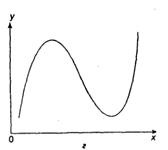
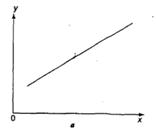
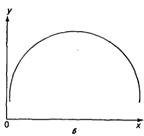
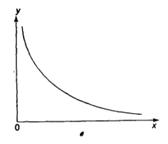
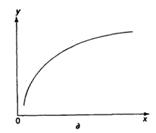
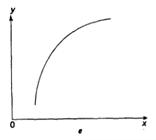
Также используется:

-

-

-

-

Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.

Пусть, например, изучается потребность предприятия в электроэнергии у в зависимости от объема выпускаемой продукции x.

Все потребление электроэнергии y можно подразделить на 2 части:

- не связанное с производством продукции (a)

- непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объемы выпуска (bx)

Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида 

Если затем разделить обе части уравнения на величину объемы выпуска продукции x, то получим выражение зависимости удельного расхода электроэнергии на единицу продукции  от объема выпущенной продукции x в виде уравнения равносторонней гиперболы

При обработке информации на компьютере выбор уравнении регрессии обычно осуществляется экспериментальным методом, т.е. путем сравнения величины остаточной дисперсии Dост рассчитанной при разных моделях.

Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии , то фактические значения результативного признака совпадают с теоретическими , т.е. они полностью обусловлены влиянием фактора x. В этом случае остаточная дисперсия Dост=0. В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических . Величина этих отклонений и лежит в основе расчета остаточной дисперсии

Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих не учитываемых в уравнении регрессии факторов, лучше уравнении регрессии подходит к исходным данным. При обработке статистических данных на компьютере перебираются разные математические функции в автоматическом режиме и из них выбирается та, для которой остаточная дисперсия является наименьшей.

Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в большей степени поддаются интерпретации и требуют меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдении должно в 6-7 раз превышать число рассчитываемых параметров при переменной x.