Вследствие того, что результат измерения Х содержит случайную погрешность D, он сам является случайной величиной.
Основной характеристикой случайной величины является функция распределения вероятностей, которая устанавливает связь между возможными значениями случайной величины и вероятностями их появления при многократных измерениях.
Существуют две формы представления этой функции: интегральная и дифференциальная.
Интегральной функцией распределения результата наблюдений является функция F(х) – вероятность того, что результат наблюдения Х окажется меньше некоторого текущего значения х: F(х)=Р{Х<х}.
Это положительная неубывающая функция (рисунок 1.3.1): 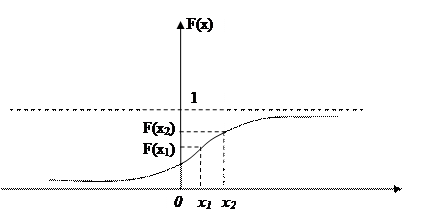
Рисунок 1.3.1 – Интегральная функция распределения результатов наблюдений
Основное свойство этой функции: вероятность того, что случайная величина принимает значения в интервале {х1, х2}, равна разности значений функции на концах интервала:
Р{х1£Х£ х2} = F(х2) - F(х1).
Если обозначить приращение х2 - х1=Dх, то одинаковым приращениям Dх соответствуют различные значения приращения вероятности DF(х). Тогда можно ввести понятие плотности распределения вероятностей случайной величины, или плотности вероятностей, которая будет иметь следующий вид:
![]() .
.
Функции распределения достаточно полно могут быть определены своими числовыми характеристиками, к которым относятся начальные и центральные моменты.
Начальным моментом является математическое ожидание случайной величины степени:
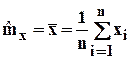 , где
, где
n – количество наблюдений.
В большинстве случаев начальный момент 1 порядка совпадает с истинным значением измеряемой величины.
Центральный момент к-порядка - математическое ожидание к-й степени центрированной случайной величины (т.е. разности между значением случайной величины и ее математическим ожиданием). Применительно к измерениям центрированная случайная величина будет случайной погрешностью:
D = ![]() = Х - Q .
= Х - Q .
Оценка математического ожидания будет состоятельной, несмещенной и эффективной оценкой истинного значения физической величины.
Состоятельной называют оценку, которая приближается к истинному значению измеряемой величины при n ®¥.
Несмещенной называется оценка, математическое ожидание которой равно истинному значению оцениваемой величины.
Эффективной является несмещенная оценка, для которой дисперсия минимальна.
Центральным моментом 2 порядка будет дисперсия результатов наблюдений:
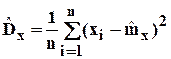 .
.
Это рассеяние результатов наблюдений относительно математического ожидания. Недостаток такого представления погрешности измерения заключается в том, что она имеет размерность квадрата измеряемой величины. Поэтому на практике используют значение среднеквадратического отклонения результата измерения
![]() .
.
В отличие от результатов измерения, числовые характеристики функции распределения являются детерминированными, а не случайными. Следовательно, чтобы найти точные значения, необходимо произвести бесконечно большое число наблюдений. Отсюда возникает задача определения приближенных значений, полученных в некотором количестве независимых наблюдений. В математической статистике такие приближенные значения, выраженные одним числом, называются ТОЧЕЧНЫМИ ОЦЕНКАМИ. Любая точечная оценка, вычисленная на основе опытных данных, представляет собой случайную величину, зависящую от самого оцениваемого параметра и от числа опытов. Распределение оценки зависит от распределения исходной случайной величины. Оценки классифицируются следующим образом:
- состоятельные, когда при увеличении числа наблюдений они приближаются к значению оцениваемого параметра;
- несмещенные, если математическое ожидание равно оцениваемому параметру;
- эффективные, если ее дисперсия меньше дисперсии любой другой оценки этого параметра.
Поможем написать любую работу на аналогичную тему

