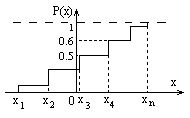Характеристики распределения случайных величин. одномерная случайная величина

С. в. Х (одномерная) - величина, могущая принять различные вероятные значения х на некотором интервале (-¥£х£¥), т.е. х - возможное значение с.в. Х.

С. в. может быть дискретной и непрерывной. Вероятностные свойства с.в. Х характеризуются интегральной функцией распределения Р(x). Значение функции Р(x) равно вероятности обнаружить с.в. Х<х (или, что то же, на интервале ‑¥, х) т.е. Р(x)=Prob(X<x), где х - конкретная детерминированная величина.

Если с.в. Х может принимать лишь дискретные значения х1, х2,...хn с вероятностями р1, р2,...рn, то функция распределения представляет собой сумму вероятностей тех значений хk, которые меньше х.

.                                                                 (12.3)

На рисунке Prob(X£x3)=Р(х3)=0,5, (т.е. Х=х1 или Х=х2 или Х=х3). Prob(X=x4)=0,6-0,5=0,1 (скачок равен вероятности появления значения х4).

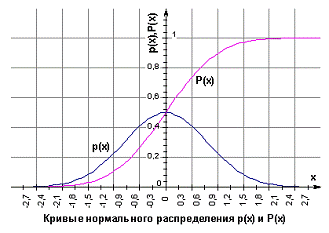Функция распределения числа m наступления события в последовательности n независимых испытаний (согласно формуле (11.2)).

Биномиальный закон распределения:

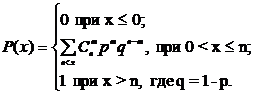        (13.3)

  .

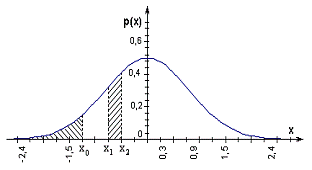
Если с.в. Х непрерывна, то функция распределения имеет вид, показанный на рисунке.

Свойства функции распределения:

1)  Р(х) - неубывающая функция аргумента х

(т.е. при x2>x1 P(x2)=Prob(X<x2)>P(x1)=Prob(X<x1));

2)  При x=-¥ P(x)=0;

3)  При x=+¥ P(x)=1;

4)  Prob(x1<X£x2)=P(x2)-P(x1)                                                                                                         (14.3);

5)  Prob(X=x1)=0. Вероятность обнаружить число, например 241.000...¥ равно 0. Однако, делая измерения, мы округляем значения, тем самым, увеличивая вероятность их появления. Например, округленное 241.0 содержит значения от 240.9500...¥ до 241.04999... ¥ и вероятность попадания числа в этот интервал не равна 0.

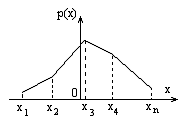Распределение с.в. Х характеризуется также функцией плотности распределения с.в. Для дискретных значений с.в. функция плотности распределения может задаваться таблично. График функции р(х)=рi при x=xi изображен на рис.  .

Т.к. возможные значения xi с.в. образуют полную группу несовместных событий (т.е. в каждом из n испытаниях с.в. обязательно примет одно из значений xi с определенной вероятностью), то , где n - число испытаний.

Для непрерывной с.в. функция плотности распределения имеет вид, показанный на рисунке.

Если функция распределения с.в. Р(х) - непрерывна, то                                (15.3)

или . По непрерывной кривой плотности распределения, в отличие от дискретной, вероятность обнаружить точное число х2 равна нулю. При помощи функции р(х) вероятность обнаружить с.в. Х в бесконечно малом интервале x<X<x+dx равна Prob(x<X<x+dx)=p(x)dx (площадь прямоугольника, dx®0). То же в конечном интервале x1<X<x2:

                                                             (16.3)

(Геометрически это заштрихованная площадь под кривой плотности распределения).

Из (15) следует, что                                                                             (17.3),

поэтому функцию распределения называют еще интегральной функцией распределения.

Свойства функции плотности распределения:

1)  Плотность распределения вероятностей - неотрицательная функция р(х)³0.

2)                                                                                                                                    (18.3),

что эквивалентно Р(¥)=1.

3) Размерность р(х) обратная размерности с.в., а Р(х) - безразмерна.

4) Числовые характеристики распределения

Математическое ожидание с.в. Х :

 - дискретной

                                                                      (19.3)

при этом               (М(x) - случайна при n¹¥).

 - непрерывной

                                                                        (20.3).

Математическое ожидание  - достоверная величина, т.к. вероятность того, что при n=¥ испытаниях мы получим среднее арифметическое М(X)= равна 1.

М(с)=с,   М(сx) = сМ(x), где с – неслучайное число.

Для независимых с.в. Х1 и Х2

М(x1+x2)=М(x1)+М(x2), М(x1x2)=М(x1)М(x2), М(x2)=2+D(x).

К математическому ожиданию стремится среднее арифметическое наблюдаемых значений с.в. при количестве испытаний n®¥. Геометрически м.о. – это абсцисса ц. т. площади под кривой плотности распределения. Размерность м.о. совпадает с размерностью с.в.

Дисперсия с.в. Х - м.о. квадрата отклонения с.в. Х от ее м.о. (центра распределения):

D(x)=M2=M(x2)-M2(x),

т.к. M2=M=M(x2)-2M2(x)+M2(x),

M=2M2(x) и M=M(x).

Дисперсия дискретной с.в. Х

                                                               (21.3)

случайна при n¹¥.

Дисперсия непрерывной с.в. Х:

                                         (22.3),

(дисперсия непрерывной с.в. - достоверна).

 - математическое ожидание.

Дисперсия характеризует разброс с.в. вокруг ее среднего значения (математического ожидания).

D(c)=0,

D(cx)=c2D(x),

D(c+x)=D(x).

Доказательство.

 D(cx)=M2=M=

c2M(x2)-M+M=

c2M(x2)-2c2M2(x)+c2M2(x)=

c2=c2D(x). D(c+x)=

M2=M2=M2=D(x).

Для независимых с.в. Х1 и Х2  D(x1±x2)=D(x1)+D(x2).

Геометрически дисперсия – это центральный момент инерции площади под кривой плотности распределения. Размерность дисперсии - квадрат размерности с.в.

Среднеквадратическое отклонение (стандарт): .

Асимметрия непрерывной с.в. Х:

                                                           (23.3).

Если с.в. Х распределена симметрично относительно своего м.о., то А(х)=0.

Коэффициент изменчивости (вариации) с.в. Х - отношение стандарта к м.о.:

                                                                   (24.3).