Оценка погрешностей при прямых измерениях

Для повышения точности измерений (если, конечно, этом есть необходимость) следует по возможности устранить математические погрешности. Это можно сделать различными способами. Если известна природа такой ошибки, и может быть определена ее величина, достаточно ввести соответствующую поправку. Это возможно, например, для исключения влияния на результат измерения таких факторов, как температура и давление воздуха, или факторов, связанных с известным недостатком измерительного инструмента (неравноплечностые рычажных весов обитым нулем прибора и т.п.). Разумеется, что вносить такого рода поправки есть смысл только в том случае, когда их величина соизмерима с величиной других ошибок, сопровождающих данные измерения.

    Можно также исключить некоторые виды систематических погрешностей, используя спецальные методы измерений. Так, влияние уже упомянутой неравноплечности весов можно устранить, взвесив исследуемое тело дважды - сначала на одной чаше весов, а затем на другой. Есть и другие способы исключения систематических погрешностей. Однако, как было отмечено выше, всегда остается ошибка; связанная с погрешностью используемого прибора, а также случайные погрешности, которые заранее учесть нельзя.

     В том случае, если погрешность прибора заведомо больше величины случайных погрешностей, присущих данному методу при данных условиях эксперимента, достаточно выполнить измерение один раз (например, при измерении обычной масштабной линейкой длины, точно изготовленной детали ). Тогда абсолютная погрешность измерения будет равна погрешности прибора. Если, наоборот, определяющей является случайная погрешность, надо уменьшить ее величину с помощью многократных измерений. Рассмотрим методику оценки случайной погрешности в этом случае.

   Предположим, что мы произвели  n  прямых измерений величины Х . Обозначим через Х1 , Х2, ... Хn  результаты отдельных измерений, которые вследствие наличия случайных погрешностей будут в общем случае неодинаковыми. В теории вероятностей доказывается, что истинное значение измеряемой величины  (при отсутствии систематических погрешностей ) равно ее среднему значению, получаемому при бесконечно большом числе измерений, т.е.

                   (1)

Поэтому наиболее близким Х истинному будет для данной серии измерений среднее арифметическое значение, а именно:

                           (2)

Отклонения измеренных значении Хn от Xср   носят случайный характер и называются абсолютными ошибками отдельных намерений :

                       (3)

    В элементарной теории ошибок, разработанной Гауссом мерой случайной погрешности отдельного измерения является так называемая средняя квадратичная погрешность, вычисляем по формуле

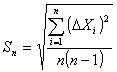                      (4)

При большом числе измерений величина  Sn стремится к некоторому пределу σ, т.е.

   Строго говоря, именно этот предел называется средней квадратичной погрешностью, а квадрат этой величины - дисперсией измерений.

   Однако средняя квадратичная погрешность отдельного измерения  Sn  полезна лишь для оценки точности применяемого способа измерений. Нас же, главным образом, интересует погрешность результата всей серии измерений. Для этого надо найти среднюю квадратичную погрешность среднего арифметического, характеризующую отклонение Хср от истинного значения искомой величины. Из закона сложения ошибок вытекает, что средняя квадратичная погрешность среднего арифметического равна

                   (5)

   Отсюда следует, что чем больше проделано измерений одной и той же величины, тем меньше случайная погрешность результата. Это вполне понятно, т.к. согласно (1) и (2), чем больше  число опытов, тем ближе  Хср  к Хист

   Используя соотношения (4) и (5) , можно записать следующее окончательное выражение для средней квадратичной погрешности результата серии измерений

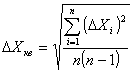                  (6)

    Это не означает, однако, что истинное значение измеряемой величины обязательно будет заключено в интервале от Xср - ΔXкв    до  Хср + ΔXкв. Оказывается, что паже при очень большом числе измерений вероятность того, что истинное значение попадет в указанный интервал, не превышает 0,7. Другими словами, надежность полученного результата в данном случае составляет около 70 %. При малом числе измерений (n < 10) она будет еде меньше.

   Вероятность того, что истинное значение измеряемой величины попадет в заданный интервал, называется доверительной вероятностью, или коэффициентом доверия  Р , а соответствующий интервал, определяемый величиной абсолютной погрешности –  доверительным интервалом. Достоверность результата при данном количестве измерений можно увеличить, уменьшая его точность, т.е. расширяя доверительный интервал.

Обычно случайную погрешность рассчитывают по формуле:

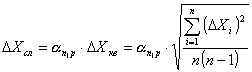                        (7)

где αn,p — коэффициент Стьюдента, зависящий от числа измерений  П.  и выбранного значения доверительной вероятности P. Значения  αn,p для ряда случаев приведены в таблице I.

Таблица I.

Как видно из таблиц, увеличение числа опытов позволяет при заданной доверительной вероятности существенно уменьшить случайную погрешность. Здесь следует учесть, что помимо коэффициента  αn,p  с ростом n уменьшается и значение  Хкв.

   Таким образом, для характеристики величины случайной погрешности в принципе необходимо задать два числа : саму погрешность Xкв и доверительную вероятность P, позволяющую оценить степень надежности полученного результата. Необходимая степень надежности определяется спецификой производимых измерений. Доверительная вероятность должна быть, например, очень высокой при контроле размеров деталей самолетов  и достаточно низкой при  аналогичном контроле деталей ручной тележки. В условиях учебной лаборатории достаточно брать P = 0,7.

   Для окончательной оценки величины абсолютной погрешности ΔХ  следует теперь сравнить полученную случайную погрешность с погрешностями других видов. Если путем многократных измерений удалось сделать случайную ошибку заметно меньше приборной ( при незначительных систематических ошибках ), то в качестве ΔХ  можно взять погрешность использовавшегося прибора. В противном случае в качестве ΔX берут значение Xсл .

Таким образом,  для оценки абсолютной погрешности при прямых измерениях следует :

1) произвести серию измерений искомой величины и вычислить среднее значение по формуле (2);

2)  вычислить абсолютные ошибки отдельных опытов согласно (3);

3)  рассчитать ΔХкв по формуле (б);

4)  определить случайную погрешность, пользуясь формулой  (7) и таблицей 1 (или формулой Стъюдента);

5)  сравнить  ΔХср  погрешность прибора, выбирая в качестве абсолютной погрешности          наибольшую из этих погрешностей;

6)  записать результат измерений в виде X = Хср ± ΔХ  (8)

   Заметим, что если величины случайной и приборной погрешностей близки друг к другу, то обе они влияют на точность результата, примерно в одинаковой степени. Поэтов иногда в мчестве максимального значения абсолютной ошибки берут сумму указанных погрешностей.

   Следует обратить внимание на то обстоятельство, что величина абсолютной погрешности сама по себе дает мало информации о действительной точности измерения, если не сопоставлять ее со значением измеряемой величины. Действительно, пусть погрешность, полученная при измерении линейных размеров, равна 0,5 см. или при этом идет речь о длине, например, спичечной коробки, то точность будет очень плохой, а если с такой же погрешностью измерена длина заводского корена, то точность измерения следует считать даже излишне высокой.

    Поэтому помимо абсолютной погрешности часто используется так называемая относительная погрешность измерения Р. Она равна отношению абсолютной погрешности измерения к среднему значению измеряемой величины :

                        (9)

  Относительную погрешность иногда выражают в процентах. Тогда:

Особенно удобно использовать относительную погрешность при сравнении точности измерений разнородных физических величин.