Оценка случайных погрешностей прямых измерений с многократными измерениями

Приемы оценки случайных погрешностей результатов измерений с многократными измерениями различны для равноточных и неравноточных измерений.

Равноточные измерения – измерения какой-либо величины, измеренные значения которых получены одним оператором, в одинаковых условиях и с помощью одного и того же СИ.

Неравноточные измерения - измерения какой-либо величины, измеренное значение которых получены разными операторами в различных условиях, с применением различных СИ (и даже различных методов измерений).

При оценке случайных погрешностей и тех и других измерений, будем полагать, что систематические погрешности тем или иным образом исключены из измеренных значений, т.е. они являются исправленными.

Приемы оценки случайных погрешностей прямых равноточных измерений стандартизированы и регламентируются нормативными документами.

За результат измерения принимается значение оценки математического ожидания           , называемое чаще средним арифметическим результатов наблюдений и обозначаемое      .

Это значение определяется по формуле

                                                                                 (4.12)

где Xi – i-е измеренное значение или показание.

Оценка (4.12) является состоятельной, несмещенной и эффективной оценкой истинного значения измеряемой величины.

Состоятельной называют оценку, которая приближается (стремится по вероятности) к истинному значению числовой вероятности оцениваемой величины при n→∞.

Несмещенной является оценка, математическое ожидание которой равно истинному значению оцениваемой величины.

Эффективной является несмещенная оценка, для которой          

Среднее квадратическое отклонение (СКО) – параметр функции распределения измеренных значений илипоказаний, характеризующий их рассеивание и равный положительному корню квадратному из дисперсии этого распределения.

Оценкой является выборочное стандартное отклонение       , определяемое по формуле:

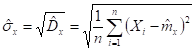                                                          (4.13)

Так как при практических расчетах вместо

    применяется его оценка    , то мы можем определить лишь значения

                                                                                                                                                                                      (4.14)

    где     - случайные отклонения результатов отдельных измеренных значений или показаний.

Следовательно, для расчета оценки СКО (      ) вместо (4.13) должна применяться следующая формула:

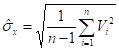                                                                           (4.15)

Известно, что оценка стандартного отклонения распределения  называется выборочным стандартным отклонением среднего арифметического и определяется по формуле:

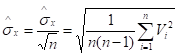               (4.16)

Значения  X   и             называются точечными и  всегда являются приближенными, так как получены на основании ограниченного числа измерений.

Кроме того, они не содержат никаких сведений о вероятности этих оценок, хотя и позволяют оценить числовые значения результата измерения и его случайного отклонения.

Поэтому теперь необходимо перейти от точечных оценок к так называемым интервальным, которое связаных с определением доверительных границ случайной погрешности результата измерения

Доверительные границы погрешность измерения        – это верхняя и нижняя границы интервала, внутри которого с заданной доверительной вероятностью Pд находится значение погрешности измерения, а, следовательно, и истинное значение измеряемой величины.

Для нахождения доверительных границ случайной погрешности необходимо умножить               на коэффициент t, зависящий в общем случае от доверительной вероятности Pд, числа наблюдений n и закона распределения измеренных значений или показаний, т.е.

                                                                                                    (4.17)                                                                 

Для наиболее универсального нормального распределения плотности вероятности случайных величин (распределения Гаусса, а для n<30 – распределения Стьюдента) значения t определены численным решением интеграла вероятности, табулированы в зависимости от       и n и приведены в справочниках и учебниках.

Значение                     следует определять для                        = 0.95 , если другое  значение     не задано.

В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих       = 0.95, допускается указывать границы для                                                             = 0.99 .

В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо       = 0.99 принимать более высокую доверительную вероятность.

При числе измеренных значений или показаний n>50 для проверки принадлежности их к нормальному распределению предпочтительным             являются            критерии           

Пирсона или      Мизеса-Смирнова.

При 15<n<50 предпочтительным является составной критерий. При n ≤ 15 принадлежность их к нормальному распределению не проверяют.

При неизвестной функции распределения или невозможности проверки принадлежности результатов наблюдений к нормальному распределению рекомендуется значение t для расчета                  определять для нормального распределения.

Оказывается, что при n ≥ 30 и P = 0.9973 - t=3. Это значение t считают предельно возможным при определении                                                                             по формуле (4.17), так как вероятность появления большего значения очень мала (0,0027). Поэтому критерий «трех сигм» принят в качестве критерия грубых погрешностей.

Если модуль случайного отклонения      окажется больше трех выборочных стандартных отклонений ряда измеренных значений или показаний       , то такое измеренное значение или показание содержит грубую погрешность и должно быть исключено из ряда при обработке.

Математически это выражается следующим образом

                                                                                                                                                                                     (4.18)