Оценка случайных погрешностей косвенных измерений с многократными измерениями

Как и в случае прямых измерений, необходимо оценить истинное значение измеряемой величины Q и доверительные границы погрешности результата косвенного измерения.

За результат косвенного измерения принимается величина     . Она вычисляется при подстановке в формулу (2.3) средних арифметических значений аргументов, полученных с помощью формулы (4.12)

                                                                (4.19)

Свойства оценок      и     аналогичны.

Выборочное стандартное отклонение результата косвенного измерения             определяется по формуле

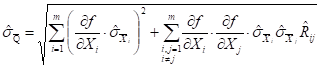                          ,                 (4.20)

где        и       - частные производные, вычисляемые при       и     ;

- оценка коэффициента корреляции между погрешностями измерения величин                       и

Величина                                (4.21)

            называется частной случайной погрешностью результата косвенного измерения.

Значение производной   при         характеризует «вес» этой погрешности в оценке  , т.е. является весовым коэффициентом (иногда он называется также коэффициентом влияния).

Коэффициент корреляции определяет, как известно, степень статистической связи между случайными величинами, в нашем случае, между случайными погрешностями измерения величин      и     .

Его возможные значения лежат в интервале

                                                                       (4.22)

1.            - случай независимых частных погрешностей. В этом случае формула (4.20) упрощается и с учетом (4.21) принимает вид

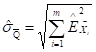                                                                                   (4.23)

2.            - случай зависимых частных погрешностей. В этом случае           определяется из общей формулы (4.20), но предварительно определяется оценка    по формуле

                                                                                                      , (4.24)

где n – наименьшее из чисел наблюдений       и       .

Если      >0 (положительная корреляция), то одна из погрешностей возрастает при увеличении другой, если же   <0 (отрицательная корреляция) – тенденция будет обратной.

Доверительные границы случайной погрешности результата косвенного измерения определяются по формуле, аналогичной формуле при прямых измерениях                                                                                                                                                                                            (4.25)

Коэффициент Стьюдента t выбирается следующим образом. Если n≥30, значение t прямо определяется из таблицы, как и при прямых измерениях. Если же n<30, то предварительно нужно определить так называемое «эффективное» число степеней свободы распределения Стьюдента, учитываемое затем при определении t из таблицы.

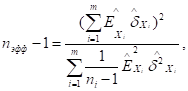                                                      (4.26)

Где: 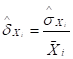 ; ni – число измеренных значений или показаний при прямых измерениях Хi

В заключение рассмотрим так называемый критерий ничтожных погрешностей.

С учетом весовых коэффициентов частные погрешности неодинаково влияют на величину суммарной погрешности косвенного измерения. Некоторые из них могут быть значительно меньше других, и они не будут оказывать заметного влияния на значение итоговой погрешности.

Такие частные погрешности называются ничтожно малыми или ничтожными.

С учетом правила округления частная погрешность считается ничтожной, если она изменяет суммарную погрешность не более чем на 5%.

Если

                                                                                                                    (4.27)

    то она считается ничтожной.

Это неравенство в метрологии называется критерием ничтожных погрешностей.

Использование критерия ничтожных погрешностей при оценке погрешностей косвенных измерений позволяет найти те величины(аргументы), повышение точности измерения которых позволит уменьшить суммарную погрешность результата измерения, и наоборот, повышать точность измерения каких величин не имеет смысла, так как их частные погрешности и без того ничтожно малы.