Сила равномерного давления на криволинейную стенку - ГИДРАВЛИКА  И ГИДРОПРИВОД. КОНСПЕКТ ЛЕКЦИИ

В этом случае элементарные силы  имеют разные направления. Главный вектор  системы вычисляется через свои проекции. Чтобы найти его проекцию  на ось х , проектируем на эту ось векторы  (рис.7).

,

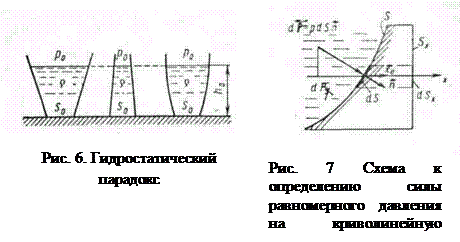где  – единичный вектор оси x; – проекция площадки dS на плоскость, нормальную оси х. Искомая величина  при

.                                 (49)

Линия действия силы  проходит через центр тяжести площади проекции . Таким образом, величина проекции на направлении оси x силы равномерного давления р на криволинейную поверхность S равна произведению давления и площади проекции Sx этой криволинейной поверхности на плоскость. нормальной оси х. Если такие проекции на три взаимно ортогональные оси пересекаются в одной точке, то система сил  может быть сведена только к силе давления, величина которой

,                                                        (50)

а направление определяется направляющими косинусами

; ; .            (51)

Если составляющие не пересекаются в одной точке, система сводится к силе и моменту.

2.3. Сила неравномерного давления на плоскую стенку (, ).

Систему элементарных сил , одинаковых по направлению, но различных по величине, можно свести в данном случае к одной силе давления

,                                                                      (52)

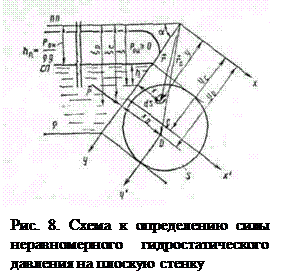где S – площадь стенки.

Величина этой силы

                                                             (53)

зависит от закона распределения давления Р по площади S. При воздействии на S капельной жидкости эти законы могут быть различными. Их конкретный вид зависит от ориентации площадки и действующих на жидкость массовых сил при абсолютном и относительном покое.

Вычислим силу  для плоской стенки, наклоненной к горизонту под углом a и подверженной  воздействию  тяжелой жидкости, находящейся в состоянии абсолютного покоя (рис. 8).

Определим результирующую силу избыточных давлений , которые создаются внешним избыточным  и весовым  давлениями. Заменим внешнее давление  воздействием эквивалентного слоя жидкости, толщина, которого  определяется высотой поднятия жидкости в пьезометре . Таким образом, внешнее давление из рассмотрения исключается, и свободная поверхность СП заменяется пьезометрической плоскостью ПП. Продолжим плоскость стенки до пересечения с пьезометрической плоскостью. Вдоль линии их пересечения направим ось х, а ось у расположим в плоскости стенки. Затем для наглядности повернем плоскость стенки на 90° вокруг оси у и совместим стенку с плоскостью чертежа.

Величину силы вычислим по формуле (53):

.

В рассматриваемом случае (см. рис. 8) давление

,                                                     (54)

что при подстановке в формулу (53) дает

.

Интеграл  представляет собой статический момент площади S относительно оси Ох, равный, как известно, произведению S на координату  ее центра тяжести.

Поэтому

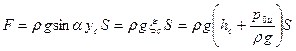.                (55)

Формула (55) может быть записана в двух видах

,                                                                          (56)

где 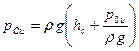 – избыточное давление в центре тяжести площади S, или

.                                                           (57)

Согласно (56) величина силы избыточного давления покоящейся жидкости на плоскую стенку равна произведению площади стенки на избыточное давление в ее центре тяжести.

Вектор силы  направлен по нормали к стенке S:

,

а линия действия этой силы пересекает стенку в некоторой точке D, называемой центром давления. Для отыскания координат этой точки () используем теорему о равенстве момента равнодействующей и суммы моментов составляющих, которая в данном случае выражается уравнением

,                                                         (58)

где  и  – радиус-векторы соответственно центра давления D и произвольной точки (ху) площади S.

По правилам составления проекций векторного произведения находим

; .

Учитывая выражения (54) и (55), получим

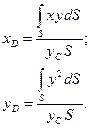                                                                     (59)

Более удобные выражения для  и  получим, если воспользуемся теоремой о соотношении между моментами второй степени, взятыми относительно параллельных осей

; ,

где – оси координат, проходящие через центр тяжести С площадки S параллельно осям х и у;  и  – координаты центра тяжести С в системе xу;  – центробежный момент площади S относительно осей х и у ;  – момент инерции площади S относительно оси х (см. рис. 8). Окончательно,

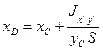; .                                     (60)

Вторая из формул (60) показывает, что центр давления расположен ниже центра тяжести на величину .

Возвращаясь к формуле (57), заметим, что силу давления в рассматриваемом случае можно получить, складывая независимо вычисленные две силы:  и , где – сила внешнего избыточного давления, – сила весового давления. При таком способе определения силы  следует помнить, что линии действия сил  и  не совпадают, и центр давления D определяется линией действия суммарной силы .