(
, 
)
В этом случае элементарные силы 
имеют разные направления. Главный вектор 
системы вычисляется через свои проекции. Чтобы найти его проекцию 
на ось х , проектируем на эту ось векторы 
(рис.7).
 |
,
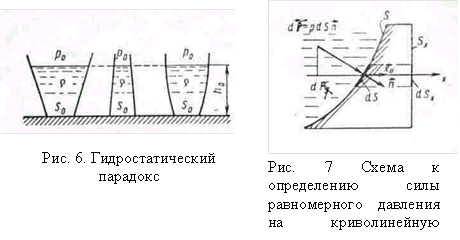где 
– единичный вектор оси x; 
– проекция площадки dS на плоскость, нормальную оси х. Искомая величина при 
. (49)
Линия действия силы проходит через центр тяжести площади проекции 
. Таким образом, величина проекции на направлении оси x силы равномерного давления р на криволинейную поверхность S равна произведению давления и площади проекции Sx этой криволинейной поверхности на плоскость. нормальной оси х. Если такие проекции на три взаимно ортогональные оси пересекаются в одной точке, то система сил может быть сведена только к силе давления, величина которой
, (50)
а направление определяется направляющими косинусами
; 
; 
. (51)
Если составляющие не пересекаются в одной точке, система сводится к силе и моменту.
Поможем написать любую работу на аналогичную тему