Мы уже говорили о том, что хаотические отступления от ньютоновского детерминизма вначале казались недоразумением, либо погрешностями опыта. Но оказалось, что реальная необратимость процессов (по Ньютону и Лапласу этого не должно быть) и есть причина отступлений от механистического описания явлений. Мы говорили о тепловом хаосе и о Максвелле – создателе статистической механики. С одной стороны теория Максвелла-Фарадея описывает обратимые процессы, а реальность (выравнивание температур в изолированной системе) убеждает в другом. Хаотичным оказалось и излучение. Но даже в классической механике (Ньютона, Лагранжа, Мопертюи) ещё Пуанкаре в задаче трех тел обнаружил, что фазовые траектории точек (рис.1) – это «ткани» с бесконечно тесными нитями. При этом ни одна из траекторий никогда не пересекает себя! То есть уже в задаче трех тел – фактическая необратимость.
Гейзенберг пришел к выводу, что при эволюционировании системы на малых отрезках времени неопределенность состояния увеличивается медленно, а на больших – сильно. Более того, и в простых ньютоновских системах возникают случайные явления, от которых не избавиться уточнением начальных условий и учетом внешних воздействий на них. Система здесь подчиняется детерминистским законам, а совершает хаотические движения. Здесь, оказывается, нет устойчивости решения задачи (карандаш не будет стоять вертикально на острие и так далее).
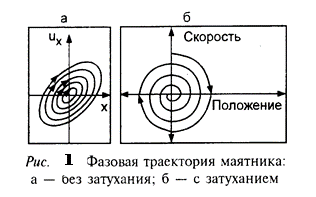Хаотические движения удобно анализировать, используя понятие фазового пространства (для движения, например, вдоль прямой по осям фазового пространства откладывают координату и скорость точки). Например, сравним траекторию в фазовом пространстве маятника (одномерное движение с изменением координаты – угла отклонения) без затухания (рис. 1а) и с затуханием (рис. 1б).
В последнем случае фазовая траектория оказывается в начале координат (состояние покоя), отвечающем положению равновесия. Эта точка – аттрактор – обобщенное понятие равновесия. При хаотическом движении фазовые траектории с близкими начальными параметрами быстро расходятся, а потом хаотически «перемешиваются». Так создаются складки. Такая область фазового пространства со складками называется странным аттрактором (с перескоками из одной области в другую, рис.2). Но эти складки возможны только в фазовом пространстве трехмерном и выше.
У странных аттракторов есть фракталы – объекты, проявляющие по мере увеличения их изображения все большее число деталей. Таковыми являются коллоиды, отложения металла на электродах при электролизе, клеточные популяции. При электролизе слой меди (для шарика) растет не пропорционально кубу расстояния, а по степенному закону с показателем 2,4. Хаос порождает фракталы, а фазовая траектория обладает для фракталов самоподобием, то есть при выделении двух близких точек на фазовой траектории фрактала и последующим увеличением масштаба траектория между этими точками наблюдается такой же хаотичной, как и вся она в целом.
4.2 Диалектика катастроф. Порядок и хаос в макросистемах.
Все самоорганизующиеся процессы имеют пороговый характер. Так, при малых скоростях течения вязкой жидкости флуктуации затухают и рассасываются. А выше порога – уже не рассасываются, достигая макромасштабов, выводя систему на новый устойчивый режим, но с новой структурой. Это уже описывается нелинейными уравнениями для системы вдали от равновесия (с несколькими решениями).
Катастрофа – это скачкообразное изменение параметров в ответ на малые изменения внешних условий (потеря устойчивости). Теория катастроф - это обобщение теории поиска экстремумов (минимумов и максимумов) на случай многих переменных. Она опирается на теорию гладких функций. У истоков ее были Пуанкаре, Ляпунов, Андронов (бифуркации), Понтрягин (ввел понятие грубости – структурной устойчивости структуры). Эта теория нашла многие применения, в том числе при исследовании биений сердца, а так же в геометрической оптике, лингвистике, геологии, гидродинамике, моделировании деятельности головного мозга и психических расстройств, политике, цензуры, в теории элементарных частиц и так далее.
Эта теория – переворот в математике и физике. Считают, что она гораздо ценнее и информативнее, чем, например, математический анализ. Она даёт, как частный случай, и теорию всех плавных процессов и позволяет свести множество сложных ситуаций к небольшому числу изученных схем, ибо глобальная природа всех явлений, по-видимому, едина.
Поможем написать любую работу на аналогичную тему