Теория катастроф описывает области устойчивости структур, а развертка статистических закономерностей во времени описывается теорией бифуркаций, – теорией удвоения, или ветвления. Речь идет о нелинейных системах, которые имеют ряд решений. При этом нужно найти, какие именно из них ответвляются от известного решения при изменении параметров. Управляющими параметрами можно вызвать катастрофические скачки состояний системы. Последовательность бифуркаций, возникающая при углублении неравновесности в этой системе, меняется и процесс может идти по разным сценариям.
Классической иллюстрацией перехода к хаосу является картина роста популяции насекомых на изолированном острове. Летом выводятся насекомые численностью Х j и откладывают яйца. На следующий год их станет Х j+1. Это число зависит линейно от Х j и от (1– Х j) (насекомые двух полов), а также от некоторого параметра скорости роста – С. При С < 1 и увеличении j (номер года) популяция вымирает.
При 1 < C < 3 ее численность приближается к значению Х = 1 – 1/С – это область стационарного состояния.
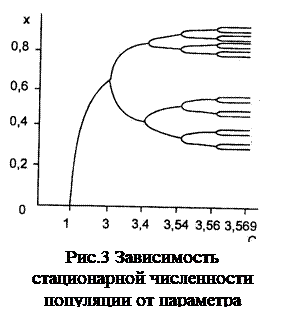
При 3 < C < 3,4 уже получается две ветви зависимости Х = Х(С) – 2 ветви решений и численность колеблется между ними (рис. 3). То есть существует диапазон значений параметра с упорядоченным и периодичным поведением системы. При этом вначале численность резко растет, откладывается много яиц. На следующий год появляется перенаселенность, резко снижается численность в следующем году. Поэтому период колебаний численности насекомых равен 2 годам.
При 3,4 < C < 3,54 – уже 4 ветви (четырех-стадийный цикл колебаний) – период удваивается и так далее. Фейгенбаум (1978) нашел универсальный закон перехода к хаосу при удвоении периода.
При С = 3,57 период стремится к бесконечности, поведение системы становится хаотичным, различные решения перекрываются.
Расчеты на ЭВМ (смотрите рис. 4) становятся некорректными (когда даже решения начинают зависеть от случайных процессов в самой машине), решения для близких начальных условий оказываются далекими. Медленное изменение параметра приводит к затягиванию потери устойчивости, но затем система скачком переходит в (само-) автоколебательный режим (рис.4).
Поможем написать любую работу на аналогичную тему