Уравнения гидродинамики заметно упрощаются в случае стационарного течения жидкости. Под стационарным (или установившимся) подразумевают такое течение, при котором в каждой точке пространства, занятого жидкостью, скорость течения остаётся постоянной во времени. Скорость 
остаётся функцией только координат
,
.
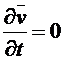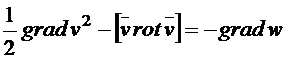Рассмотрим некоторые сведения о линиях тока. Линии тока это линии, касательные к которым указывают направление вектора скорости в точке касания в данный момент времени. Уравнения линий тока определяются системой дифференциальных уравнений
.
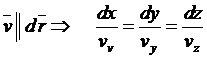При стационарном движении жидкости линии тока остаются неизменными во времени и совпадают с траекториями частиц жидкости.
При нестационарном течении такое совпадение не имеет места:
- касательные к линии тока дают направление скорости различных частиц жидкости в последовательных точках пространства в определённый момент времени
- касательные к траектории дают направление скорости определённых частиц в последовательные моменты времени.
Умножим уравнение Эйлера для стационарного потока жидкости на единичный вектор касательной к линии тока в каждой её точке 
.
Проекция градиента на некоторое направление равна производной, взятой по этому направлению. Поэтому
.
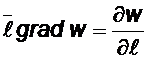Вектор 
перпендикулярен вектору скорости, и поэтому его проекция на направление 
равна нулю
.
Таким образом, получаем
.
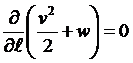Откуда следует, что величина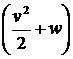 
постоянна вдоль линии тока
.
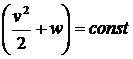Значение const, вообще говоря, различно для разных линий тока. Это уравнение называют уравнением Бернулли.
Если течение жидкости происходит в поле сил тяжести, то в правой части уравнений Эйлера есть ускорение силы тяжести 
.
Выберем направление силы тяжести в качестве направления оси z, причём положительные значения z отсчитываются вверх. Тогда проекция 
на 
есть
.
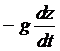Соответственно этому будем иметь
.
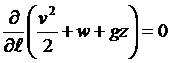Таким образом, уравнение Бернулли гласит, что вдоль линий тока остаётся постоянной длина
.
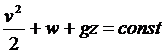Поможем написать любую работу на аналогичную тему