Внезапное расширение трубопровода

Рассмотрим потерю напора при внезапном расширении потока. Пусть поток несжимаемой жидкости течет в горизонтальной трубе, претерпевающей резкое увеличение площади поперечного сечения от величины S1 до S2 ( рис. 47 ).

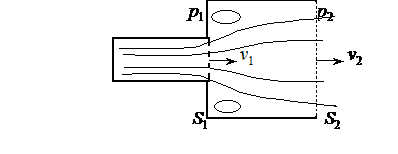
Рис. 47

Пусть скорость течения уменьшается при этом от v1 до v2.

          Массовый расход остается одинаковым в обоих сечениях

.

          Секундное количество движения в сечении 1, ограничивающем рассматриваемый элемент потока слева, равен

,

где  - поправка к количеству движения на неравномерное распределение скоростей в сечении.

          Сечение 2, ограничивающее элемент потока справа, выбираем в таком удалении от внезапного расширения, где возмущение течения, вызванные в потоке расширением русла, можно полагать успокоенным. В этом сечении секундное количество движения равно

.

          Сила давления, действующая на выделенный элемент потока, равна:

,

где p1, p2  - давления в сечениях 1 и 2.

          В проекции на ось трубы будет иметь следующее равенство

или

,

откуда

.  (*)

          Уравнение Бернулли для двух сечений имеет следующий вид

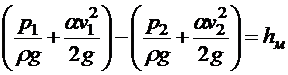
или

.

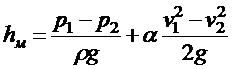          На основании (*) имеем

.

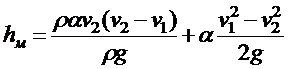          Если положить a=1, что верно для большинства турбулентных потоков, то

.

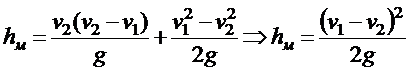          Это положение, известное под название теоремы Борда, формулируется так:

          Теорема Борда. Потеря напора при внезапном расширении потока равна скоростному напору, вычисленному по потерянной  скорости.

          Для других видов местных сопротивлений потеря напора определяется по формуле, аналогичной внезапному расширению

.

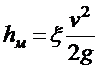          Безразмерный коэффициент x, входящий в формулу, называется коэффициентом местного сопротивления.

          Значение этого коэффициента зависит от конструкции местного сопротивления, которая определяет характер отрыва потока от обтекаемых внутренних полостей и интенсивности возникающих при этом вихреобразований.

          Часто при определении потерь напора на местные сопротивления оказывается удобным введение так называемой эквивалентной длины детали трубопровода.

          Эквивалентной длиной данного местного сопротивления называют такую длину прямого отрезка трубы, которая создает гидравлическое сопротивление, равное сопротивлению детали трубопровода, обусловившей потери напора.

          Пусть Lэ - эквивалентная длина данного местного сопротивления, потеря напора на прямом участке трубы длиной Lэ  по формуле равна

.

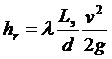          По условию эквивалентности должно быть  hr=hм, откуда 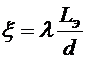, следовательно

.

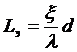          Таким образом, эквивалентная длина местного сопротивления выражается через диаметр трубы, поэтому, например, говорят, что сопротивление углового вентиля эквивалентно сопротивлению участка трубы того же диаметра длиной, равной 200 диаметрам трубы.

Пусть требуется определить потерю напора в трубопроводе, состоящем из прямых отрезков труб, соединенных между собой с помощью всевозможных фасонных частей, с включением различного рода задвижек, вентилей, клапанов и т.д. Эту задачу можно решить, определяя по формулам и таблицам из справочников, коэффициенты местных сопротивлений x1, x2,…, xт или вычислив предварительно эквивалентные длины местных сопротивлений.

          В первом случае потеря напора может быть определена по формуле

,

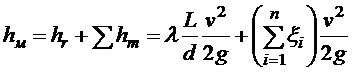а во втором - по формуле

.

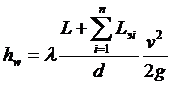          Исследованию местных коэффициентов сопротивлений посвящается обширная литература, проделано огромное количество опытов, однако до сих пор задача о местных сопротивлениях остается разрешенной еще не полностью.

          Можно считать доказанным, что величина местного сопротивления при ламинарном течении меняется в зависимости от числа Re, при турбулентном режиме она остается почти постоянной при любых Re.