Бесциркуляционное обтекание цилиндра

          Наложим плоский параллельный оси ox однородный поток со скоростью  и комплексным потенциалом ( рис. 63 )

на скоростное поле диполя с комплексным потенциалом

 ,

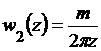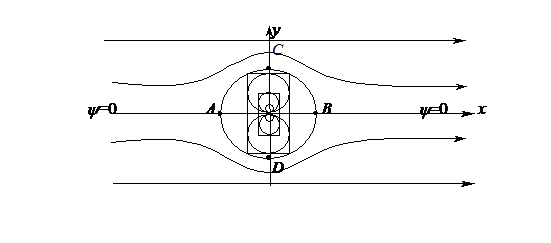
Рис. 63

 .

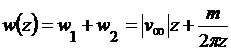Для определения функции тока отделим мнимую часть

 .

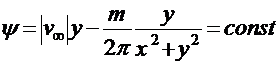Нулевая линия тока

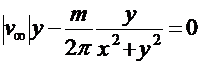
представляет собой две кривые :

          1) окружность  ,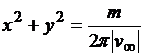

          2) ось ox   y = 0.

          Выберем произвольную до сих пор величину момента диполя равной

 .

          Получим нулевую линию тока в виде совокупности окружности радиуса а с центром в начале координат и оси ox.

          Остальные линии тока

 .

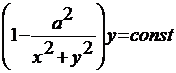          Движение происходит в двух областях - вне и внутри круга.

          Течение вне круга можем рассматривать как обтекание круглого цилиндра, с радиусом основания равным а плоскопараллельным потоком, имеющим на бесконечности скорость .

          Такому потоку соответствует комплексный потенциал

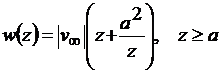
          Остановимся подробнее на внешнем течении. Найдём распределение скоростей в области .

          Найдём распределение скоростей на поверхности цилиндра

,

 .

          Определим модуль скорости на контуре круга

.

          Отсюда следует, что при плоском безвихревом обтекании кругового цилиндра идеальной жидкостью скорость распределена по закону синуса.

          Максимальная скорость при

 .

          Используя уравнение Бернулли, можно найти распределение давления

,

 ,

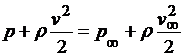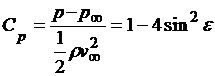где Cp - коэффициент давления.

На рис. 64 показано распределение коэффициента давления по поверхности цилиндра.

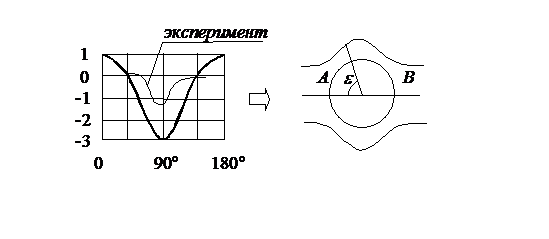
а                                              б

Рис. 64