Циркуляционное обтекание цилиндра

          Циркуляционное обтекание цилиндра можно получить, если наложить на рассмотренное выше течение чисто циркуляционный поток от плоского вихря, расположенного в начале координат с направлением вращения по часовой стрелке. Сложив комплексные потенциалы указанных потоков, получим

.

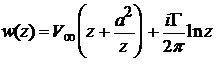          Наложение циркуляционного потока нарушает симметрию линий тока, так как на верхней поверхности скорость от чисто циркуляционного потока направлена в ту же сторону, что и скорость бесциркуляционного потока, а внизу скорость чисто циркуляционного потока направлена в обратную сторону. Вследствие сложения скоростей над цилиндром образуется область повышенных скоростей, а под цилиндром - пониженных.

          Суммарная скорость потока на поверхности цилиндра

 .

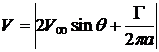          Положение критических точек А и В можно найти приравняв нулю скорость потока. Тогда

 .

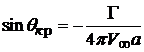          Для    имеем две критические точки  А и В ( рис. ) . При увеличении  G  критические точки смещаются вниз. В случае, когда , получаем  , то есть критические точки сливаются в одну точку. При дальнейшем увеличении  Г , то есть , критическая точка сходит с цилиндра.

          Найдем распределение давления по поверхности цилиндра. Используя уравнение Бернулли, соотношение для коэффициента давления и распределение скорости на поверхности цилиндра, имеем

.

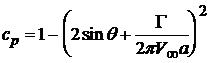          Из соотношения следует, что распределение коэффициента давления симметрично относительно оси  у.  Поэтому при циркуляционном обтекании цилиндра, так же как при  Г = 0, сопротивление равно нулю :  Ха = 0 ( парадокс Даламбера ). При этом подъемная сила не равна нулю. Она определяется по формуле Жуковского.