Первый закон термодинамики

          Пусть некоторое количество газа находится в равновесии. Обозначим через dQ количество подведённой к газу извне теплоты. В общем случае подвод теплоты приводит к изменению внутренней энергии газа dU и объёма. При изменении объёма газ совершает внешнюю работу, равную dL=pdV. Поэтому

,

или, относя все величины к 1 кг массы газа, получаем

,

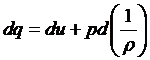где dq - суммарная теплота, подведенная к 1 кг массы газа извне, du - изменение внутренней энергии 1 кг массы газа, 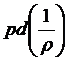 - работа, затрачиваемая на расширение ( 1 / r - объём, занимаемый 1 кг массы газа).

          При постоянном объёме dV = 0, dQ=dU или dq=du, т.е. вся теплота, подводимая к газу, тратится на увеличение его внутренней энергии. Поэтому

.

          Пренебрегая зависимостью cV от температуры и имея в виду, что при T=0   u = 0, имеем

.

Внутренняя энергия является одной из функций состояния газа.

Используя формулы

.

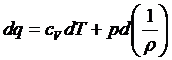          Уравнение является математическим выражением первого закона термодинамики.

          Энтальпия. Введём ещё одну функцию состояния i, определяемую соотношением

.

          Или, пренебрегая изменением cp,

.

          Эта функция называется энтальпией. Из определения энтальпии следует, что её приращение di представляет собой приращение теплоты dq в процессе p=const. Имея это в виду, из первого закона термодинамики 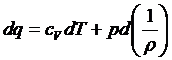, интегрируя его в предположении p=const, получим

.

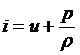          Используя уравнение состояния и соотношение , имеем

.

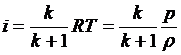          Энтропия. При изучении течения газа часто используют понятие энтропии. Эта функция определяется дифференциальным соотношением

.

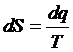Найдём связь между энтропией и энтальпией

,

из первого закона термодинамики

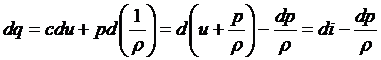
следует

 .

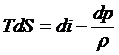          При скоростях движения жидкости сравнимых со скоростью звука или их превышающих, на первый план выдвигаются эффекты, связанные с сжимаемостью жидкости. Такое движение на практике наблюдается в газах. Поэтому о гидродинамике больших скоростей говорят обычно как о газодинамике.

          Чаще всего в газодинамике приходится иметь дело с очень высокими значениями чисел Рейнольдса. За исключением отдельных случаев ( наиболее ярким из которых является отрыв сверхзвукового потока ) при высоких значениях числа Рейнольдса вязкость оказывается не существенной для движения газа практически во всем пространстве. Поэтому в газодинамике часто  газ рассматривают как идеальную жидкость.

          Движение газа имеет существенно различный характер в зависимости от того, является оно дозвуковым или сверхзвуковым.

          С изучением сверхзвуковых течений связано решение ряда практических проблем, возникающих при создании самолетов, ракет, турбин, снарядов, аэродинамических труб для получения потоков со сверхзвуковыми скоростями.