Гидростатическое давление и его свойства - Основы гидравлики

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практические приложения.

Согласно закону внутреннего трения Ньютона, в неподвижной жидкости касательные напряжения t равны 0, так как dV = 0. Растягивающие нормальные напряжения, даже самые незначительные, приводят жидкость в движение, поэтому в неподвижной жидкости они тоже отсутствуют. Таким образом, в неподвижной жидкости действуют только нормальные сжимающие поверхностные (гидростатическое давление) и массовые силы.

Гидростатическое давление обладает двумя свойствами:

– оно всегда направлено по нормали к площадке, на которую действует (из самого определения давления);

– его величина не зависит от направления, то есть ориентации площадки в жидкости.

Докажем последнее утверждение. Рассмотрим равновесие объема жидкости в виде тетраэдра с ребрами, параллельными координатным осям и соответственно равными dx, dy, dz (Рис. 2). Пусть в выделенном объеме действует единичная массовая сила, составляющие которой равны X, Y, Z. Обозначим гидростатические давления, действующие на грани тетраэдра, параллельные координатным осям соответственно px, py и pz, а давление на наклонную грань – pn. Отметим, что все эти давления направлены по нормалям к соответствующим площадкам. Площадь наклонной грани обозначим dS. Запишем уравнение равновесия выделенного объема жидкости вдоль оси x.

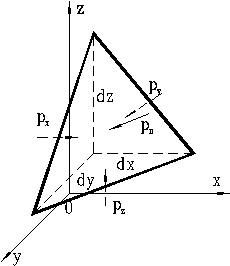
Рис. 2. Схема для доказательства свойства гидростатического давления

+

,

где первые два слагаемых – проекции на ось x поверхностных сил, а третье – массовая сила, равная массе выделенного объема жидкости, умноженной на единичную массовую силу, направленную вдоль оси x. Разделим это уравнение на площадь грани, нормальной к оси x,

. Тогда получим

.

При dx ® 0 третье слагаемое в уравнении стремится к 0, тогда .

Аналогичные выкладки можно проделать еще дважды, рассматривая равновесие объема жидкости вдоль осей y и z. Тогда получим:

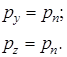
Таким образом,                    

Так как размеры тетраэдра dx, dy и dz взяты произвольно, то и наклон площадки dS произволен, и, следовательно, в пределе при стягивании тетраэдра в точку давление в этой точке по всем направлениям будет одинаковым.

Этим свойством обладает и движущаяся идеальная (лишенная вязкости) жидкость. В реальной, то есть вязкой жидкости, при движении будут возникать касательные напряжения, поэтому давление в реальной движущейся жидкости этим свойством не обладает.