Пусть на неподвижную жидкость действует только одна массовая сила – сила тяжести. Свободная поверхность жидкости представляет собой плоскость (размеры рассматриваемого объема жидкости не соизмеримы с размерами Земли). На свободную поверхность действует давление p0. Найдем давление в произвольной точке M, расположенной на глубине h (Рис. 3). Выделим около этой точки горизонтальную элементарную площадку dS и построим на ней вертикальный цилиндрический объем высотой h.
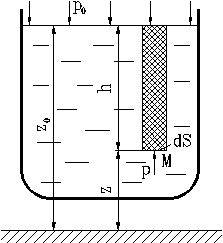
Рис. 3. Схема для вывода основного уравнения гидростатики
Рассмотрим уравнение равновесия этого объема в вертикальном направлении:
![]()
Сократив и перегруппировав слагаемые, получим основное уравнение гидростатики:
![]() .
.
По этому уравнению можно вычислить давление в неподвижной жидкости на любой глубине. Мы видим, что давление в жидкости складывается из давления на внешнюю поверхность и давления, создаваемого весом вышележащих слоев жидкости.
Величина p0 одинакова для всех точек объема жидкости, поэтому, учитывая свойство гидростатического давления, можно сформулировать закон Паскаля: давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково.
Как мы видим, с увеличением глубины погружения давление возрастает по линейному закону и на данной глубине есть величина постоянная. Поверхность, во всех точках которой давление одинаково называется поверхностью уровня. Как мы видим, эта поверхность – плоскость, параллельная свободной поверхности.
Если от произвольного уровня отложить вертикальные координаты точки M (z) и свободной поверхности (z0) и заменить h = z0 – z , то получим другую форму записи основного уравнения гидростатики:
![]() или
или
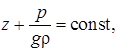
где z – геометрический напор (высота);
![]() – пьезометрический напор (высота).
– пьезометрический напор (высота).
Сумма геометрического и пьезометрического напоров – это гидростатический напор. Таким образом, гидростатический напор для всего объема неподвижной жидкости есть величина постоянная.
Поможем написать любую работу на аналогичную тему

