В некоторых случаях в гидравлике удобно использовать уравнение количества движения, например, когда надо рассчитать силу воздействия движущегося потока на преграду или русло, не рассматривая процессы внутри потока жидкости.
Для материального тела массой m, движущегося со скоростью V, изменение количества движения за время dt вследствие силы F выразится векторным уравнением 
где 
– приращение количества движения, обусловленное импульсом 
Применим эту теорему механики к участку потока (Рис. 41) с расходом Q между сечениями 1 – 1 и 2 – 2 в условиях установившегося течения. За время dt этот участок сместится в положение 1’ – 1’ и 2’ – 2’. Изменение количества движения будет равно разности количеств движения заштрихованных участков потока: 
. Импульс сил – 
,
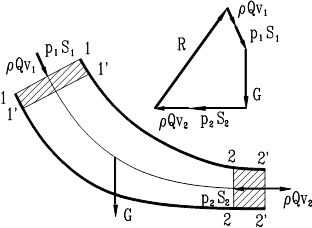
Рис. 41. Применение уравнения
импульса к жидкости
где 
– вес всего участка потока; 
– реакция русла.
Тогда
=.
Сократив на dt, получим
=
.
Таким образом, вектор равнодействующей всех внешних сил, действующих на жидкость в фиксированном объеме, равен геометрической разности количеств движения жидкости, вытекающей из объема и втекающей в него за единицу времени. В этом состоит теорема Эйлера об изменении количества движения жидкого объема.
Можно уравнение переписать так:
и построить замкнутый многоугольник векторов, в котором направление вектора 
надо изменить на противоположное, так как его надо в векторном уравнении взять со знаком “минус”.
Это же уравнение можно записать в проекциях на ту или иную ось.
В качестве примера вычислим силу воздействия потока жидкости на преграду. Пусть жидкость вытекает в атмосферу и наталкивается на безграничную стенку, установленную нормально к оси потока. В результате жидкость растекается по преграде, изменяя направление движения на 90°. Известны площадь потока S, плотность жидкости r и скорость истечения V.
По теореме Эйлера, учитывая, что давление в струе и на стенке равно атмосферному, получим уравнение в проекции на ось потока
– F = – rQV = – rV 2S.
Следовательно, F = rV 2S.
Поможем написать любую работу на аналогичную тему