Простым трубопроводом называют трубопровод постоянного диаметра, если он не имеет ответвлений. Простые трубопроводы могут соединяться последовательно, параллельно или образовывать разветвления.
Жидкость движется по трубопроводу благодаря тому, что энергия жидкости в его начале, больше, чем в конце. Это может быть обеспечено либо работой насоса, либо разностью уровней жидкости, либо давлением газа (газобаллонная подача жидкости).
Пусть имеется простой трубопровод, представленный на Рис. 35. В нем имеется ряд местных сопротивлений.
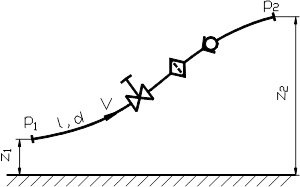
Рис. 35. Схема простого
трубопровода
z1 и z2 – геометрические высоты начала и конца трубопровода;
p1 и p2 – давления в этих сечениях;
l, d – длина и диаметр трубопровода;
V – скорость жидкости.
Запишем уравнение Бернулли для первого и второго сечения:
.
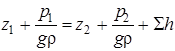Так как диаметр трубы постоянен, то скорости будут в этих сечениях равны. Равны будут и коэффициенты Кориолиса a1 = a2, поэтому равные скоростные напоры в уравнении можно опустить.
Выразим пьезометрический напор в начальном сечении трубопровода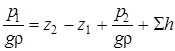 
.
Величину p1/gr назовем потребным напором Hпотр, если эта величина неизвестна, если же она задана, то – располагаемым напором Hрасп. Разность геометрических высот Dz = z2 – z1 вместе с пьезометрическим напором в конечном сечении составляют статический напор:
.
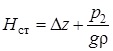Запишем потери напора в трубопроводе как степенную функцию расхода Sh = KQ m, где K – сопротивление трубопровода и m имеют разные значения в зависимости от режима течения.
Для ламинарного режима
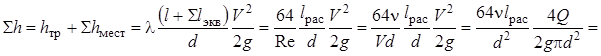
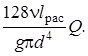
Таким образом,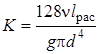 
, а m = 1.
Для турбулентного режима
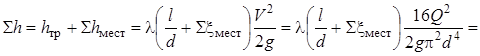
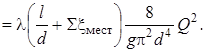
То есть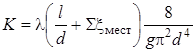 
, а m = 2.
Таким образом, 
. При ламинарном режиме – это уравнение прямой , а при турбулентном – параболы (Рис. 36).
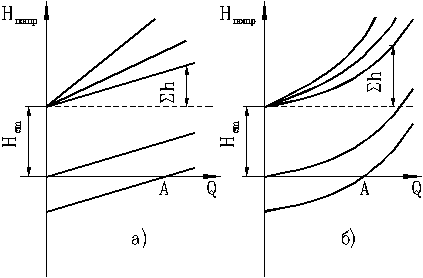
Рис. 36. Зависимость потребных напоров от расхода жидкости
в трубопроводе
На рисунке приведены кривые потребного напора для 5 разных трубопроводов при ламинарном (а) и турбулентном (б) режимах течения. Чем больший расход жидкости требуется подать по трубопроводу, тем больше должен быть потребный напор. Статический напор может иметь и положительное и отрицательное значение. Если Hст< 0, то можно наблюдать движение жидкости самотеком с расходом, соответствующим точке A. Крутизна кривых потребного напора зависит от K и возрастает с увеличением местных сопротивлений, длины трубопровода и уменьшением его диаметра.
Кривая потребного напора, построенная при Hст= 0, называется характеристикой трубопровода.
Пользуясь кривыми потребного напора, решают следующие типы задач:
- по известным расходу Q, давлению на выходе из трубы p2, свойствам жидкости (r и n), размерам трубопровода, местным сопротивлениям, а также материалу и качеству поверхности трубы находят потребный напор Hпотр;
- по известным располагаемому напору Hрасп, давлению на выходе из трубы p2, свойствам жидкости (r и n), размерам трубопровода, местным сопротивлениям, а также материалу и качеству поверхности трубы находят расход жидкости Q;
- по известным расходу Q, располагаемому напору Hпотр, давлению на выходе из трубы p2, свойствам жидкости (r и n), размерам трубопровода, кроме диаметра, местным сопротивлениям, а также материалу и качеству поверхности трубы находят диаметр трубы d.
Поможем написать любую работу на аналогичную тему