Основные виды местных сопротивлений. Определение коэффициента местных потерь

В уже рассматривался вопрос о расчете потерь напора на местных сопротивлениях, то есть таких участках трубопровода, где вследствие изменения размеров или конфигурации русла, происходит изменение скорости потока, отрыв его от стенок и возникают вихри. Рассмотрим местные сопротивления подробнее.

Простейшие местные гидравлические сопротивления можно разделить на три группы: расширения, сужения и повороты русла. Каждое из них может быть внезапным или постепенным. Более сложные случаи местных сопротивлений – это комбинации этих простейших сопротивлений. Например, в вентиле поток сначала искривляется, сужается и, наконец, расширяется.

При турбулентном режиме течения коэффициенты потерь x определяются в основном формой местных сопротивлений, а от числа Рейнольдса Re практически не зависят, поэтому величина местных потерь пропорциональна квадрату скорости. Такую зависимость называют квадратичной. Значения коэффициентов потерь x находят в основном опытным путем, хотя для некоторых простейших местных сопротивлений их удается получить теоретическим путем. При решении практических задач значения x находят в справочниках, где они приведены в виде формул, таблиц, графиков для различных видов местных сопротивлений.

Для большинства местных сопротивлений в трубопроводах при  Re ³ 105 имеет место турбулентная автомодельность – потери напора пропорциональны скорости во второй степени и коэффициент местного сопротивления не зависит от Re. В местных сопротивлениях, где происходит резкое изменение сечения трубопровода и образуются значительные вихри, автомодельность устанавливается и при Re ³ 104.  Например, для внезапного расширения трубопровода 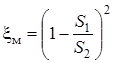, где S1 и S2 – площади трубопровода до и после внезапного расширения. Для выхода трубопровода в бак S2 >> S1, поэтому xм » 1. При постепенном расширении потока в диффузоре коэффициент местного сопротивления

,

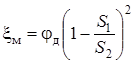где j д – коэффициент потерь.

При внезапном сужении трубы 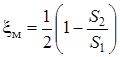. Для входа в трубопровод из бака S1 >> S2, поэтому xм » 0,5.

При ламинарном режиме течения местные потери обычно малы по сравнению с потерями на трение, а закон сопротивления более сложный, чем при турбулентном режиме:

где hтр – потери напора, обусловленные непосредственно действием сил трения (вязкости) в данном местном сопротивлении и пропорциональные вязкости жидкости и скорости в первой степени; hвихр – потери, связанные с отрывом потока и вихреобразованием в самом местном сопротивлении или за ним и пропорциональные скорости во второй степени.

Таким образом, коэффициент потерь при ламинарном режиме можно представить как сумму:

где A и B – безразмерные константы, зависящие в основном от формы местного сопротивления.

В зависимости от значения Re и формы местного сопротивления потери напора при ламинарном режиме могут выражаться как линейной, так и квадратичной от скорости зависимостью, а также какой-то средней между ними кривой. Значения коэффициентов A и B следует искать в справочнике в зависимости от вида местного сопротивления и его параметров.