Расходом называется количество жидкости, протекающее через живое сечение потока (струйки) в единицу времени. Количество жидкости можно задать объемом, массой или весом. Соответственно и расходы бывают объемный Q, массовый Qm и весовой QG.
Для элементарной струйки, имеющей бесконечно малые площади живых сечений, можно считать скорость жидкости в любой точке сечения одинаковой. Тогда
dQ = V dS; dQm=r dQ = rV dS; dQG= g dQm= grV dS,
где dS – площадь живого сечения струйки.
Для потока конечных размеров скорость в различных точках сечения будет различной, поэтому расход следует определять как сумму элементарных расходов струек
![]()
Но это чисто теоретическая формула, воспользоваться ей для определения расхода проблематично. Обычно вводят в рассмотрение среднюю по сечению скорость потока, которую можно найти по измерянному расходу
![]() , откуда Q = VcpS.
, откуда Q = VcpS.
Основываясь на законе сохранения вещества, на предположении о неразрывности (сплошности) потока и на свойстве непроницаемости трубки тока, для стационарного течения несжимаемой жидкости можно утверждать, что объемный расход во всех сечениях элементарной струйки один и тот же:
dQ = V1 dS1 = V2 dS2 = const (вдоль струйки).
Это уравнение объемного расхода для элементарной струйки.
Аналогичное уравнение можно записать и для потока конечных размеров, ограниченного непроницаемыми стенками, только скорости следует брать средние
Q = Vср1 S1 = Vсp2 S2 = const (вдоль потока).
Из последнего уравнения следует, что средние скорости в потоке несжимаемой жидкости обратно пропорциональны площадям живых сечений:
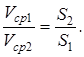
Уравнение расхода – это частный случай закона сохранения вещества для условий неразрывности потока.
Поможем написать любую работу на аналогичную тему

