Определение сил гидростатического давления покоящейся жидкости на плоские стенки.

Определим как рассчитывается сила гидростатического давления на плоскую стенку, которая наклонена под углом , при одностороннем воздействии жидкости . Одну координатную ось направим вдоль стенки, а другую по линии пересечения стенки со свободной поверхностью. Для удобства развернем проекцию стенки в плоскость чертежа. Выделим на ней фигуру площадью  .   Между любой  координатой  у  и  глубиной погружения h существует следующая связь: .

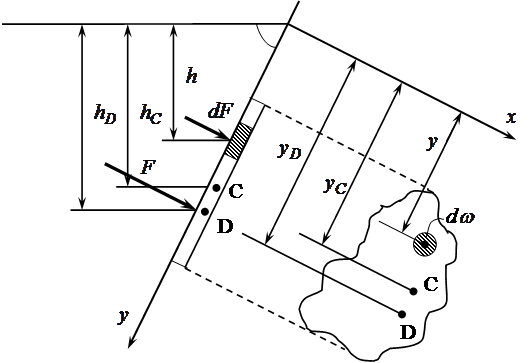
 Рисунок - К определению силы давления на плоскую стенку.

На каждый бесконечно малый элемент площади  действует элементарная сила , но давление в центре тяжести  равно .

Тогда элементарная сила .

Суммарная сила давления на всю площадь со может быть получена интегрированием по площади :

,

где  - статический момент площади относительно оси ОХ.

Известно, что статический момент площади равен произведению координаты центра тяжести на площадь фигуры:

,

откуда можно записать, что суммарная сила гидростатического давления равна:

   или   ,

где  - давление в центре тяжести.

Таким образом, сила гидростатического давления на плоскую поверхность равна произведению гидростатического давления в центре тяжести этой поверхности на ее площадь.

Центром давления называется точка приложения полной силы гидростатического давления, действующей на данную поверхность.

Для определения положения центра давления воспользуемся известной теоремой статики: момент равнодействующей силы равен сумме моментов сил ее составляющих.

Т.е.                                                     .

Из этого выражения можно найти искомую координату центра давления (точки D):

,

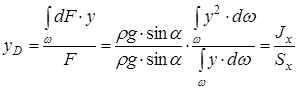где  - момент инерции площади относительно оси ОХ.

Но момент инерции относительно любой оси может быть выражен через момент инерции относительно центральной оси  (оси, проходящей через центр тяжести фигуры).

,

где а - расстояние между осями (в нашем случае )

Тогда 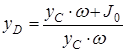                             или                 .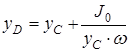

Используя уравнение связи между глубиной h и координатой y, получим уравнение для определения глубины погружения центра давления:

.

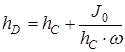Это выражение показывает, что центр давления лежит всегда ниже центра тяжести (кроме давления на горизонтальную плоскость, когда они совпадают).