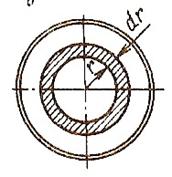
Рассмотрим кольцевой слой жидкости толщины dr на расстоянии r от оси трубы, площадь сечения кольца равна dω=2πr dr, а расход жидкости через это сечение равен:
dQ=u dr= u2πr dr
Подставляя сюда выражение скорости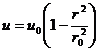 
и интегрируя, получим:
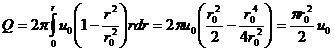, т.е. 
.
Это есть выражение расхода через осевую скорость в трубе.
С другой стороны 
, где v-средняя скорость в живом сечении потока.
=> 
.Т.о., средняя скорость потока при лам.режиме равна половине осевой.
С учетом этого результата из выражения для потерь напора на трение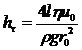 
можно получить выражение для потерь напора по длине l в виде: 
или, введя вместо радиуса диаметр трубы и выражая абсолютную вязкость η через кинематическую (η=v∙ρ), в виде 
.
Из этой формулы видно, что потери напора при ламинарном движении пропорциональны первой степени средней скорости или расхода жидкости.
Эту формулу можно представить в другом виде, если учесть, что 
.
Делая соответствующую подстановку, получим 
Или, введя обозначение 
, окончательно получим 
Это универсальная формула Вейсбаха-Дарси,
где λ - коэффициент гидравлического трения или коэф. гидравлического сопротивления.
Формула Дарси-Вейсбаха используется для определения потерь на трение как для ламинарного, так и для турбулентного течения, однако, если для ламинарного движения коэффициент гидравлического сопротивления λ вычисляется по формуле λ=64/Re, то для турбулентного движения формулы будут иметь другой вид.
Поможем написать любую работу на аналогичную тему