Модели управления запасами, помогают на два возможных вопроса, которые предъявляются к складируемому изделию:
1) когда размешать заказ на изделие,
2) как много изделий надо заказывать для пополнения запаса.
Рассмотрим четыре модели запасов, не зависящих от спроса
1. Модель экономичного (по количеству) заказа (EOQ),
2. Модель производственного (по количеству) заказа,
3. Модель заказа с резервным запасом;
4. Модель с дисконтируемым количеством
Основная модель экономичного заказа (EOQ). Экономичный заказ является одной из старейших и наиболее част используемых техник управления запасом. Этой техникой легко пользоваться, но она требует многих допущений. Наиболее существенные допущения следующие.
1 Спрос известен и постоянен
2 Текущее время, время между размещением заказа и получением заказа известно и постоянно.
3 Получение заказа немедленное Другими словами, заказанный запас поступает в одной партии, в одно время.
4 Понижение (дисконт) количества невозможно.
5 Переменными являются только затраты на переналадку или размещение заказа (затраты на переналадку) и затраты на хранение или складирование запасов во времени (затраты хранения, или текущие затраты)
6 Дефицит (нехватка) совершенно исключены, если заказ размещен вовремя.
Расчетный механизм этой модели основан на оптимизации совокупных операционных затрат по закупке и хранению запасов на предприятии. Эти операционные затраты предварительно разделяются на две группы:
а) сумма затрат по размещению заказов (включающих расходы по транспортированию и приемке товаров)
ОПП
ОЗрз = ----------- х Срз , где
РПП
ОЗрз - сумма операционных затрат по размещению заказов;
Срз - средняя стоимость размещения одного заказа;
ОПП – объем производственного потребления товаров в рассматриваемом периоде;
РПП – средний размер одной партии поставки товаров.
Из приведенной формулы видно, что при неизменном объеме производственного потребления и средней стоимости размещения одного заказа общая сумма операционных затрат по размещению заказов минимизируется с ростом среднего размера одной партии поставки товаров.
б) сумма затрат по хранению товаров на складе.
РПП
ОЗхт = ------------- х Сх , где
2
ОЗхт - сумма операционных затрат по хранению товаров на складе;
Сх - стоимость хранения единицы товара в рассматриваемом периоде.
Из приведенной формулы видно, что при неизменной стоимости хранения единицы товара в рассматриваемом периоде общая сумма операционных затрат по хранению товарных запасов на складе минимизируется при снижении среднего размера одной партии поставки товаров.
Т.о. с ростом среднего размера одной партии поставки товаров снижаются ОЗрз и возрастают ОЗхт. Данная модель позволяет оптимизировать пропорции между этими двумя группами затрат так, чтобы их совокупная сумма была минимальной.
затраты
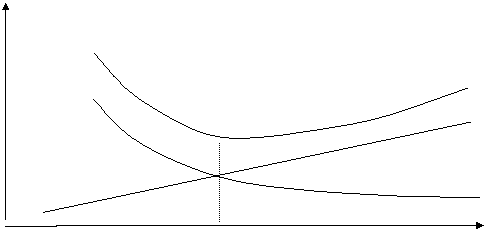
Суммарные затраты
Затраты на хранение
Стоимость выполнения заказа
Оптим. запас Размер запаса
Рис. 5.3 .Определение экономичного (оптимального) запаса
Математически данная модель выражается формулой:
2*ОПП*Срз
РППо = Ö ¾¾¾¾¾¾ , где
Сх
РППо - оптимальный средний размер партии поставки товаров.
Модель производственного (по количеству) заказа. В предыдущей модели управления запасом мы предполагали, что все количество единиц заказа поступало одновременно. Однако встречаются случаи, когда фирма может пополнять ее запасы в течение определенного периода времени. Такие случаи требуют использования иной модели, которая исключает предположение об одновременности получения заказа. Эта модель используется, когда запасы непрерывно поступают и восстанавливаются через определенное время, т. е. когда изделия производятся и продаются одновременно. В таких условиях мы должны принять во внимание дневную производительность (или скорость притока запаса) и скорость дневного расхода запаса. Рис. 5.4 показывает уровень запасов как функцию времени.
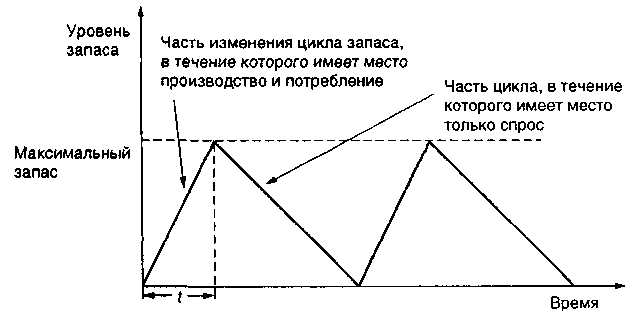
Рис. 5.4. Изменение уровня запаса во времени в производственной модели
Поскольку эта модель, главным образом, подходит для использования в производственной ситуации, она часто называется моделью производственного заказа. Она хорошо себя проявляет, когда запасы наращиваются в течение времени, и традиционный показатель экономичного уровня заказа уже предположительно установлен. Мы получим эту модель, полагая затраты на заказ или переналадку, равными затратам на хранение, рассчитанным для РППо.
2*ОПП*Срз
РППо = Ö ¾¾¾¾¾¾¾¾ , где
Сх*(1- ОПП/МП)
МП – мощность поставщика в рассматриваемом периоде.
Модель заказа с резервным запасом. В ряде моделей запасов мы не можем позволить возникновения нехватки запасов или, иначе говоря, мы не можем допустить хранения, которое не соответствовало бы текущему спросу.
Предполагаем, что возможны нехватки и поэтому возможны страховые запасы, чтобы избежать нехватки. Модели, отражающие такое состояние производства, называются моделями заказа с резервным запасом, или моделями, планирующими нехватку запаса (рис.5.5).
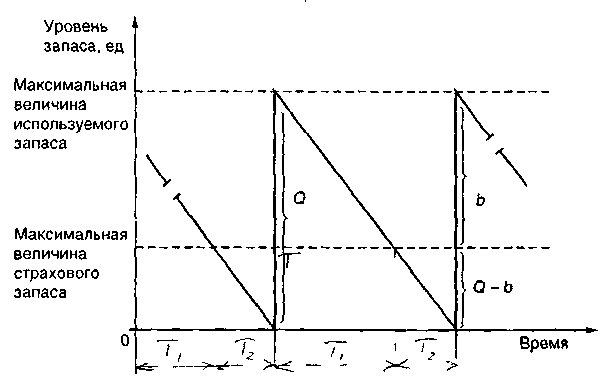
Рис. 5.5. Изменение запаса во времени с учетом страхового запаса
Основные допущения для этой модели — тс же, что и для предыдущих моделей. В дополнение, однако, мы допускаем, что продажи не будут потеряны из-за запасов. Мы будем использовать те же измерения, что и прежде, дополнив их переменной Сх.сз — затратами единицы страхового запаса. Тогда:
2*ОПП*Срз Сх+ Сх.сз
РППо = Ö ¾¾¾¾¾¾¾ * ¾¾¾¾¾
Сх Сх.сз
Модели с дисконтируемым количеством. Чтобы увеличить объемы продаж, многие компании предлагают своим покупателям дисконтирование по количеству Количественный дисконт — это просто снижение цены единицы Р, когда товар покупается в больших количествах.
Поскольку стоимость единицы для большего дисконта обычно является наименьшей, может появиться искушение сделать заказ больше, чтобы выиграть на понижении цены изделия. Размещая заказ по величине с наибольшей дисконтной ценой, с другой стороны, можно не достичь минимизации общих затрат на запасы. При увеличении дисконтируемого количества затраты на продукт падают, но при этом растут затраты на хранение, поскольку заказ становится большим. Поэтому наибольший выигрыш достигается, когда значение количественного дисконта рассматривается между понижающейся стоимостью продукта и увеличивающимися затратами хранения. С включением затрат на приобретение продукта в расчет уравнение, определяющее общие годовые затраты, примет вид:
(Общие затраты) = (Затраты переналадки) + + (затраты хранения) + (затраты продукта)
Теперь мы можем определить количество, которое будет соответствовать минимальным общим годовым затратам Процесс поиска решения состоит из четырех шагов, потому что имеется несколько дисконтов.
1 Для каждого значения дисконта рассчитываем величину РППо используя следующее уравнение
2*ОПП*Срз
РППо = Ö ¾¾¾¾¾¾ , где
I*P
Здесь затраты хранения (Сх = IP) выражены в виде процента I от цены единицы продукта Р вместо того, чтобы рассматривать их как постоянную величину, приходящуюся на единицу продукта в год Сх.
2 Для любого дисконта, если заказываемое количество слишком мало, чтобы быть дисконтированным, изменим заказываемое количество в сторону его увеличения до ближайшей минимальной величины, которую уже можно будет продисконтировать.
3 Используя уравнение для общих затрат рассчитаем общие затраты для каждого РППо.
4 Отберем то РППо, которое соответствует минимальным затратам.
Поможем написать любую работу на аналогичную тему

