Оптимальная производств. Партия (модель производства партии продукции)

Модель производства партии продукции

В предыдущих разделах рассматривались модели "управления запасами, в которых предполагалось, что использование запасов происходило после того, как весь объем товаров был получен (произведен). Таким образом, максимальный объем запасов на складе совпадал с объемом заказа. Характерные ситуации, адекватные такой модели, представлены в торговой деятельности.

Для многих случаев на производстве характерными являются ситуации, когда партия деталей, производимых на одном станке, сразу же используется в производстве на другом станке с меньшей производительностью (скоростью). Поэтому максимальный объем запасов не будет совпадать с размером заказа. Для определения оптимального количества заказа возможно использование формулы для ОРЗ. При этом необходимо определить средние постоянные запасы. Иллюстрация такого подхода представлена на рисунке 2.1.

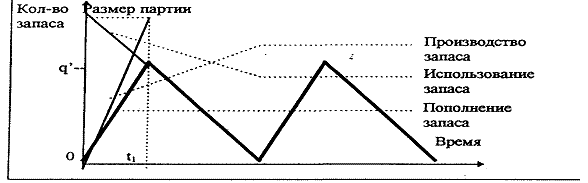
Рис. 2.1. Модель производства партии продукции

В такой ситуации не происходит скачкообразного изменения запасов на величину заказа.

ПОСТРОЕНИЕ МОДЕЛИ: Введем обозначения:

Р - уровень производства (количество единиц продукции, выпускаемой за отчетный период);

D - потребность (спрос) на выпускаемый товар;

Q - размер одной производственной партии в натуральных показателях;

Q/P - период времени, за который будет произведена одна партия товара;

Q/D - период времени между запусками производства;

Chl = P*Ch - стоимость хранения единицы товара за отчетный период;

Со1 - стоимость перезапуска производства - фиксированные затраты, зависящие от количества запусков производства .(по аналогии со стоимостью размещения одного заказа).

Предположим, что спрос постоянный и определенный, продукция выпускается равномерно в течение периода Q/P и поступает на склад непрерывно и равномерно в течение периода производства.

АЛГОРИТМ РЕШЕНИЯ

Для решения данной задачи воспользуемся выводами, полученными в теории оптимального размера заказа.

Готовая продукция убывает со скоростью "D".

Во время производственного цикла продукция пребывает со скоростью "Р" и одновременно убывает со скоростью "D", в итоге так как P>D, продукция пребывает со скоростью "P-D".

Максимальный уровень продукции на складе, равен (время производственного цикла * скорость пребывания продукции на складе)= Q/P*(P-D)=Q((P-D)/P) и достигается в конце производственного цикла.

Зная максимальный уровень продукции на складе мы можем рассчитать среднее количество продукции на складе, которое будет равно:

,                                            (1.30)

Когда суммарные затраты на хранение будут равны

,                                      (1.31)

Суммарные затраты, зависящие от размера производственной партии определяются по формуле:

,              (1.32)

Как и в теории оптимального размера заказа - оптимальный размер производственной партии будет наблюдаться при равенстве затрат на хранение и на перезапуск производства. Минимум функции соответствует такому объему заказа (производства), где производная равна нулю. Продифференцировав функцию общих затрат ТС по q и приравняв ее нулю, получим:

,                                                        (1.33)

• Формула для оптимального размера партии содержит уравнение для оптимального размера заказа и поправочный коэффициент:

,                                                   (1.34)

• Если Р очень большой (т.е. вся производственная партия производится или поступает на склад одномоментно), то значение коэффициента примерно равно единице и оптимальная производственная партия примерно равна оптимальному размеру заказа.

• Если Р близко по значению к D, то значение коэффициента, а, следовательно, и оптимальной производственной партии, стремится к бесконечности или, к непрерывному производству. В такой ситуации для управления готовой продукцией обращаются к методам управления уровнем производства, в зависимости от колебаний спроса и запасов готовой продукции.