Во многих случаях при закупке товаров у поставщиков экономически выгоднее бывает допустить отсутствие товаров в течение какого-либо промежутка времени, чем поддерживать их постоянное наличие. Для управления запасами в таких системах используется модель, в которой в течение определенного времени запас отсутствует. При этом возможны два варианта:
1. В рамках первого подхода дефицит товаров восполняется по заказам покупателей из следующей поставки. В этом случае максимальная величина запасов равна разнице объема заказа и максимального неудовлетворенного спроса, возникающего в течение времени дефицита (Q-d)
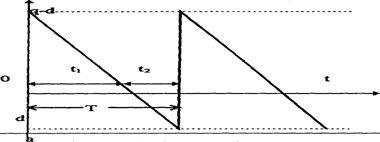
Рис. 1.11. Уровень запасов от времени.
Цикл запаса Т состоит из времени потребления запасов t1 и отсутствия запасов t2. Таким образом, в течение цикла запаса Т на складе хранится следующее количество запасов:
, (1.16)
где q – оптимальный размер заказа; d – максимальный размер дефицита.
Аналогично определяется средний уровень дефицита в течение времени t2 по формуле:
, (1.17)
В условиях известного и линейного спроса D за период (год) количество заказанных партий товара будет составлять D/q, а интервал заказа будет определяться следующей формулой:
, (1.18)
Таким образом, можно определить t1 и t2.
, (1.19)
, (1.20)
Определяем вид уравнения общей стоимости, включающий три составные части:
1) сумму затрат на подачу заказа = число заказов в год * стоимость подачи одного заказа Col=(D/q)*Col; (1.21)
2) сумму затрат по хранению = средний уровень запасов * стоимость хранения единицы запасов за год Chl = ((q-d)2/2q*Ch1; (1.22)
3) сумму издержек отсутствия запасов = средний уровень дефицита * стоимость отсутствия единицы запаса за год
Cd =(d2/2q)*Cd1 (1.23)
Суммарные затраты на заказ будут определяться следующей формулой:
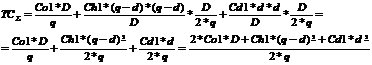(1.24)
Для минимизации данной функции, уравнение необходимо продифференцировать по двум независимым переменным q и d.
Оптимальный заказ равен
, (1.25)
а максимальный размер дефицита составит
, (1.26)
2. В рамках второго подхода спрос, возникающий на товары в течение времени дефицита, не удовлетворяется. Поэтому максимальный уровень запасов совпадает с объемом заказа. Расчеты общей стоимости запасов будут аналогичны приведенным выше, с учетом замены (q-d) на q и q на (q+d).
В этом случае уравнение общей стоимости примет вид
, (1.27)
Применяя операцию дифференцирования по частям получаем оптимальный размер заказа
, (1.28)
, (1.29)
Поможем написать любую работу на аналогичную тему