Предложенные модели управления запасами основаны на детерминированности поведения покупателей и поставщиков. Другими словами, считается полностью определенным в любой момент времени спрос на продукцию и сроки поставки заказов. В системах управления запасами, основанных на детерминированности, т.е. точном определении условий хозяйствования, размер повторного заказа, а также время его размещения являются константами; момент размещения и уровень запасов при повторном заказе определяют единственную точку повторного заказа.
На практике в условиях рыночного хозяйствования огромную роль играет фактор неопределенности. Поэтому применение детерминированных моделей ограничено. В таких ситуациях необходимо применение других подходов, учитывающих неопределенность спроса и времени поставок. Обе эти величины колеблются во времени и могут не быть постоянными и строго фиксированными. В таких случаях необходимо применение недетерминированных моделей, учитывающих фактор риска.
Наиболее распространен вероятностный подход к решению данной задачи. При построении вероятностных моделей предполагается, что спрос имеет характеристики стандартных статистических распределений (нормального, Пуассона и др.). В таких моделях вводится понятие уровня обслуживания, т.е. вероятности нехватки запасов в течение одного цикла запаса. Если величина уровня обслуживания задана, то в условиях неопределенности спроса достичь ее можно повышением уровня повторного заказа, прибавив к среднему спросу величину резервного запаса. В этих случаях необходимо компенсировать возрастание стоимости хранения запасов снижением стоимости их нехватки.
Наиболее известны два подхода к определению резервного запаса. Возможно установление уровня запасов, по достижении которого выдается новый фиксированный заказ, включающий в себя и резерв. Такой заказ выдается нерегулярно, т.е. через неравные промежутки времени, но на одинаковую величину. Либо определяется интервал времени, через который регулярно делается заказ для достижения фиксированного уровня запасов, включающего и резерв. В данном случае заказы выдаются через одинаковые промежутки времени, но на разную величину. Как правило, выбирается одна из двух моделей, учитывающих неопределенность:
1. Уровневая модель повторного заказа (метод постоянного заказа). При этом заказ выдается при снижении запасов до фиксированного уровня через неравные промежутки времени, обусловленные неравномерностью спроса.
2. Циклическая модель повторного заказа (метод постоянного периода). При этом заказ выдается на разное количество продукции через строго фиксированные промежутки времени.
При использовании любой модели необходимо определить критерий оптимизации системы управления. В данном случае рассматриваются критерий достижения необходимого уровня обслуживания ( вероятности нехватки) - максимум эффекта , либо критерий минимизации стоимости запасов - минимум затрат.
q МЕТОД ПОСТОЯННОГО ПЕРИОДА
- Время между размещением заказов постоянно и равно оптимальному периоду
- Потребность и время поставки переменные
- Величина заказа непостоянна и равна разности между целевым запасом и остатком запасов на складе в момент размещения нового заказа
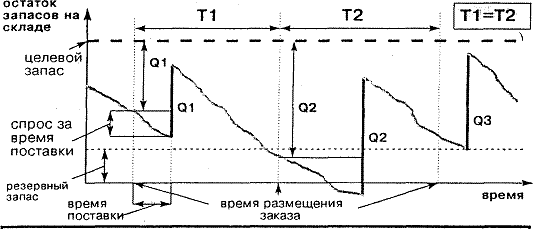
Рис. 1.12. Метод постоянного периода
УСЛОВИЯ ПРИМЕНИМОСТИ МЕТОДА ПОСТОЯННОГО ПЕРИОДА
ПРЕИМУЩЕСТВА
- Состояние запасов отслеживается только один раз в течение оптимального периода.
- Позволяет предсказать и спланировать время занятости персонала, приводит к более ритмичной работе, требует меньшей загрузки персонала.
- Возможна ситуация, когда будут образовываться группы товаров с одинаковым оптимальным периодом и одним и тем же временем перезаказа, что приведет к дополнительной экономии затрат на управлении.
- Возможна организация комбинированного заказа, что приводит к экономии затрат на выполнение заказов
НЕДОСТАТКИ
- Требует более высокого уровня резервного запаса (чем метод постоянного заказа), что приводит к завышению затрат на хранение.
- Непостоянный размер заказа может оказаться неудобным для поставщиков
ü Применим для не дорогостоящих товаров (категории В и С), а так же для товаров с высокой оборачиваемостью и для позиций со значительными колебаниями потребности. Привлекателен при возможности комбинированного заказа.
ü При использовании для дорогостоящих позиций необходим тщательный анализ соотношения затрат на хранение и других видов затрат.
Оптимальный период (Т) между размещением заказа рассчитывается на основании метода определения оптимального размера заказа (1.7).
- формула определения оптимального размера заказа
Т = Q / D = 
Целевой запас должен обеспечивать такой уровень запасов, чтобы удовлетворить потребность до следующего поступления товара на склад с учетом переменности потребности и времени поставки.
|
Резервный запас при данном методе управления запасами будет больше чем в методе постоянного заказа, так как промежуток времени, на котором приходится учитывать неопределенность потребности, становится больше на время оптимального периода и, следовательно, неопределенность потребности тоже становится больше.
q МЕТОД ПОСТОЯННОГО ЗАКАЗА
- Новый заказ размещается при достижении остатка на складе точки перезаказа.
- Потребность и время поставки переменные
- Величина заказа постоянна и равна оптимальному размеру заказа
ТОЧКА ПЕРЕЗАКАЗА = резервный запас + средняя потребность за среднее время поставки
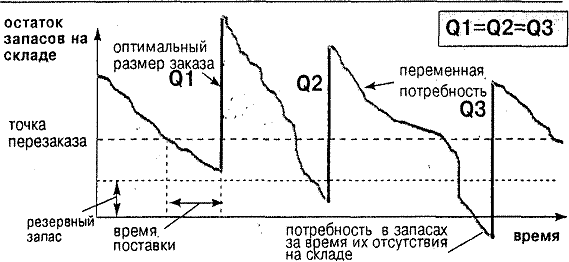
Рис.1.13. Метод постоянного заказа
УСЛОВИЯ ПРИМЕНИМОСТИ МЕТОДА ПОСТОЯННОГО ЗАКАЗА
ПРЕИМУЩЕСТВА
- Требует меньшего резервного запаса и, следовательно, приводит к более низкому уровню затрат на хранение запасов
- Постоянный размер заказа более удобен для поставщиков товара (может лучше планировать отгрузку) и для персонала (менее вероятна ошибка в размере заказа).
- Удобен для товаров с низкой оборачиваемостью.
НЕДОСТАТКИ
- Постоянно отслеживается состояние запасов, для определения точки перезаказа
- Высокие затраты на управление (особенно для товаров с высокой оборачиваемостью, т.е. при большом количестве операций за единицу времени).
- Недостаточно эффективен при значительных колебаниях потребности, так, например, если отгрузка товара, вызвавшая перезаказ, достаточно велика, то это может привести к тому, что оптимальный размер заказа может не перекрыть точку перезаказа, в этом случае придется размещать двойной или тройной заказ
ü Применим для дорогостоящих товаров (категория А), с большими затратами на хранение, а также для товаров с низкой оборачиваемостью.
ü Неприменим для товаров с большим .уровнем колебаний потребности и для товаров с высокой оборачиваемостью.
ü Для дорогостоящих и, одновременно, высокооборотных позиций необходимо оптимизировать соотношение затрат на хранение и на управление запасами.
q ПРОСТЕЙШИЕ МЕТОДЫ РАСЧЕТА РЕЗЕРВНОГО ЗАПАСА
Рассмотрим простейшие, практические методы определения точки перезаказа при использовании метода постоянного заказа:
Метод наихудшего случая. Проанализировав информацию за максимально возможное время, найдем максимальную потребность в конкретном виде запасов за время поставки. Если за это время не было дефицита запасов, то найдем минимальный уровень запасов за исследуемый промежуток. Точка перезаказа будет равна максимальному спросу за время поставки за вычетом минимального уровня запасов.
Метод допустимого количества раз отсутствия запасов. Предположим, что мы имеем данные о 30 циклах перезаказа на конкретный вид запасов, которые длились 2 года и критерий, который мы выбрали, - 2 отсутствия запасов в течение года. Проранжируем спрос за время поставки по убыванию. При выбранном критерии точка перезаказа будет находиться между 4 и 5 максимальным уровнем спроса за время поставки. Такой уровень точки перезаказа обеспечит защиту от непредвиденного спроса в 26 случаях из 30. Мы оставляем возможность отсутствия запасов на складе 4 раза за 2 года или 2 раза в год.
q АНАЛИТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА РЕЗЕРВНОГО ЗАПАСА
Размер резервного запаса зависит от степени неопределенности потребности в запасах за время поставки, степени неопределенности времени поставки и от необходимого оптимального уровня защиты от дефицита запасов, таким образом, резервный запас можно представить следующей формулой:
РЕЗЕРВНЫЙ ЗАПАС = k * sL
,
э
где sL - среднее квадратичное отклонение потребности в данном виде запасов за время поставки; при расчете учитывается как неопределенность потребности, так и неопределенность времени поставки.
В методе постоянного заказа sL рассчитывается за время поставки
В методе постоянного периода sL рассчитывается за период, равный:
время поставки + оптимальный период, так как данный период больше, то sL будет больше, чем при использовании метода постоянного заказа;
k - коэффициент безопасности - характеризует уровень защиты от дефицита запасов.
МЕТОДЫ РАСЧЕТА КОЭФФИЦИЕНТА БЕЗОПАСНОСТИ
Существует два основных подхода к определению коэффициента безопасности: статистический и экономический.
Статистические методы, основанные на необходимом уровне сервиса:
- вероятность дефицита запасов за один цикл оборота запасов (или за период между двумя перезаказами),
- вероятность удовлетворения спроса,
- уровень готовности - характеризуется периодом, во время которого запасы должны быть "положительными",
- оптимальная частота дефицита запасов за отчетный период.
Экономические методы, основанные на оптимизации затрат:
- допустимый уровень убытков вследствие отсутствия запасов на складе,
- оптимальное соотношении затрат на хранение и убытков вследствие отсутствия запасов на складе.
Рассмотрим подробнее метод постоянного заказа в упрощенном виде.
Необходимо определить значение резервного запаса, для которого будет оптимальным соотношение затрат на хранение и убытков вследствие дефицита запасов.
Рассмотрим решение данной задачи при использовании системы управления запасами на основании метода постоянного заказа. Размер резервного запаса будет определять величину точки перезаказа. Решение данной проблемы не будет сказываться на оптимальном размере заказа, а будет влиять только на изменение точки перезаказа. Следовательно, мы оптимизируем два вида затрат:
Затраты на хранение резервного запаса, которые являются частью суммарных затрат на хранение и которые будут равны:
ТС=Сh1*R, (1.35)
где Сh1 - затраты на хранение 1 единицы запасов за отчетный период, R - величина резервного запаса
Убытки вследствие дефицита запасов, которые равны
U = Cd1*S*r, (1.36)
где Cd1 - убытки вследствие дефицита 1 единицы запасов на с кладе, S - вероятное количество раз дефицита запасов за отчетный период, r - средний объем дефицита запасов в единицах.
В данной задаче мы рассматриваем убытки вследствие дефицита запасов, которые не зависят от длительности дефицита, а зависят от объема дефицита и количества дефицитов за отчетный период. Модель, в которой данные убытки зависят от продолжительности дефицита, требует более сложных расчетов.
Алгоритм решения основан на методике маржинального или предельного анализа. В данной методике мы добавляем (или отнимаем) от исследуемого параметра по единице и анализируем влияние этого изменения на оптимизируемую величину. Если это влияние положительно, то мы продолжаем изменять этот параметр в том же направлении, пока оно не уменьшится до нуля. Если влияние отрицательно, то мы изменяем параметр в другом направлении и двигаемся опять до нулевого влияния. При нулевом влиянии значение параметра оптимально. Алгоритм расчета показан на рис. 1.14. Данная методика достаточно часто применяется при нахождении оптимальных решений в экономическом анализе. Рис. 1.14. Алгоритм расчета коэффициента безопасности
Положительный вклад (выигрыш-экономия затрат на хранение) от каждой дополнительной единицы будет оставаться постоянным при уменьшении резервного запаса.
Отрицательный вклад (потери-убытки вследствие дефицита запасов) от каждой дополнительной единицы будет увеличиваться при уменьшении резервного запаса, так как будет расти вероятность дефицита запасов (S)
Выигрыш больше потерь, тогда при уменьшении резервного запаса на каждую единицу мы получаем дополнительную прибыль до тех пор, пока выигрыш будет больше потерь.
Потери больше выигрыша, тогда увеличение резервного запаса приводит к уменьшению убытков.
Оптимальный размер резервного запаса получается при условии:
S*Cd1=Ch1, (1.37)
При этом условии (1.37) выигрыш равен потерям.
Полный алгоритм расчета оптимизации затрат можно интерпретировать
рис. 1.15.
Рис.1.15. Пример расчета коэффициента безопасности методом оптимизации затрат.
• Если нам известны затраты на хранение (С) и убытки вследствие дефицита запасов (SU), мы можем подсчитать оптимальную частоту возникновения дефицита запасов за отчетный период, при которой суммарные затраты будут минимальны:
SCd1=Ch1 S=Ch1/Cd1 - формула для расчета оптимальной частоты дефицита запасов.
• Зная оптимальную частоту дефицита запасов за отчетный период(S) и частоту заказов (N), мы можем рассчитать вероятность дефицита запасов (Р) за один цикл оборота запасов (или между двумя перезаказами):
P=S/N -формула для расчета вероятности дефицита запасов за один период оборота запасов.
• Величина (Р) непосредственно связана с коэффициентом безопасности (k) на основании правила нормального распределения вероятности. Коэффициент безопасности определяется на основании специальных таблиц, которые можно найти в любой литературе по управлению запасами.
• Определив коэффициент безопасности (k) и рассчитав среднее квадратичное отклонение (sL) потребности в запасах, мы получаем оптимальное значение резервного запаса, при котором соотношение затрат на хранение и убытков вследствие дефицита запасов будет оптимальным:
резервный запас = k*sL.
q УРОВНЕВАЯ СИСТЕМА ПОВТОРНОГО ЗАКАЗА
Рассмотрим подробнее метод постоянного заказа
1.Критерий достижения заданного уровня обслуживания (эффекта)
В соответствии с данным подходом величина резервного запаса выбирается таким образом, чтобы при заданных характеристиках изменения спроса вероятность нехватки запасов была не выше заданной. Алгоритм определения резервного запаса следующий:
определяются вероятностные характеристики спроса на основе статистических наблюдений. Если спрос имеет нормальное распределение, то достаточно определить его среднее значение М =
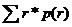(М единиц в год) и дисперсию V= s2=
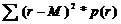, а также задается вероятность нехватки запасов - h.2. Фиксируется время поставки t.
3. Определяется среднее значение спроса Mt=M*t и дисперсия его за время поставки Vt=V*t.
4. Если бы спрос был детерминирован, то размер повторного заказа совпадал с величиной Mt. Так как спрос имеет распределение, то необходимо выбрать размер заказа R, чтобы вероятность «попадания» спроса в интервал левее R (спрос меньше запасов) была не менее 1-h. Для этого по таблицам нормального распределения определяем величину стандартизованного отклонения z = (R-Mt)/ s, при которой вероятность или площадь под «хвостом» (правее R) будет равна h.
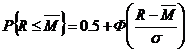
Отсюда определим значение R величины повторного заказа, и (R - Mi)- размер резервного запаса.
5. Если стоимость нехватки запасов незначительна, то общая переменная стоимость запасов будет равна сумме стоимости заказов и стоимости хранения запасов с учетом резервного запаса:
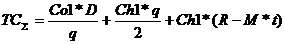.2. Критерий достижения минимума стоимости.
Цель задачи - определить резервный запас при условии минимизации стоимости. При этом общая стоимость запасов будет включать стоимость подачи заказов, стоимость хранения стандартного запаса q, стоимость хранения резервного запаса r, стоимость нехватки запасов:
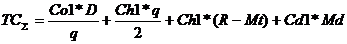,где Сd1 - стоимость нехватки одной единицы запаса, Мd - математическое ожидание количества единиц продукции, составляющей нехватку запасов в год.
Минимизируя данную стоимость мы должны выбрать такой размер резерва (R - Mt), при котором возрастание стоимости его хранения компенсируется уменьшением количества единиц нехватки (и, соответственно стоимости нехватки). Т.е. найти такой размер резерва, при котором достигается минимум суммы третьего и четвертого членов уравнения общей стоимости.
Пример
Промышленная компания использует детали А, которые закупает у поставщика. Время поставки составляет 8 дней. Спрос на них периодически меняется. Стоимость заказа составляет 27,8, стоимость хранения одной детали 0,1, стоимость срочной закупки деталей составляет 1 на единицу деталей. В году 250 рабочих дней.
Пусть определено среднее значение спроса за время поставки М=640 и среднее отклонение s =28.
Определим экономичный размер заказа для фиксированного спроса в 640/8*250=20000 единиц продукции в год.
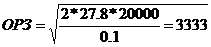. Количество заказов при этом будет равно 20000/3333 =6
Составим таблицу следующего вида:
Таблица 1.2.
Приближенное значение спроса в течение поставки
Вероятность появления этой величины спроса:
Резервный запас
640
650
660
670
680
690
700
710
720
0,135 *
0,134
0,109
0.082
0,052
0,03
0,016
0,007
0,003
0
10
20
30
40
50
60
70
80
Величина вероятности в графе 2 вычисляется следующим образом:
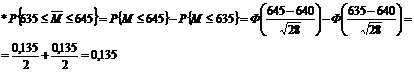
Так как в качестве шага исследования спроса выбрана величина 10, то имеется в виду, что величине спроса в 640 соответствует интервал спроса от 635 до 645, величине спроса в 650 соответствует интервал спроса от 645 до 655 и т.д. Поэтому, используя стандартизованное отклонение, можно определить вероятность попадания этого стандартизованного отклонения в такой интервал спроса.
Далее для каждой величины резервного запаса вычисляется математическое ожидание количества единиц нехватки запаса в течение одного цикла поставки. Такая величина равна вероятности увеличения спроса от среднего больше, чем величина резервного запаса, умноженной на количество единиц нехватки при этом спросе и сумме этих возможных ситуаций.
Таблица 1.3.
Математическое ожидание числа нехватке запасов
Стоимость
Резервный запас
Удовлетворенный спрос
в течение цикла
в течение года
нехватки запасов
резервного запаса
Суммарная
80
720
0
0
0
80*0,1
8
70
710
10*0,003=0,03
0,03*6= 0,18
0,18*1= 0,18
70*0,1=7
7,18
60
700
10*0,007+
20 *0,003=0,13
0,13*6= 0,78
0,78*1= 0,78
60*0,1 =6
6,78
50
690
10*0,16+
+20*0,007
+30*0,003=0,39
0,39*6= 2,34
2,34*1= 2,34
50*0,1=5
7,34
40
680
10*0,03*+
+20*0,016+
+30*0,007+
+40*0,003=0,95
0,95*6= 5,7
5,7*1= 5,7
40*0,1=4
9,7
В приведенных расчетах предполагалось, что спрос не бывает выше 720 деталей за время поставки.
Как видно из расчетов, минимальная сумма стоимости нехватки запасов и стоимости хранения резерва составляет 6,78 при величине резервного фонда в 60 единиц.
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проектуУзнать стоимость