Виды стратегии финансирования текущих активов

Как было показано в предыдущей главе, ликвидность и приемлемая эффективность текущих активов в значительной степени определяются уровнем чистого оборотного капитала. Если исходить из вполне реальной посылки, что краткосрочная задолженность не может быть источником покрытия основных средств, то очевидно, что значение этого показателя меняется от нуля до некоторой максимальной величины М. При нулевом значении показателя «чистый оборотный капитал» риск потери ликвидности достигает максимального значения; с ростом значения этого показателя риск убывает. Максимального значения М чистый оборотный капитал теоретически может достигнуть в том случае, если отсутствует краткосрочная кредиторская задолженность. В этом случае М равно стоимости текущих активов, а риск потери ликвидности равен нулю.

В теории финансового менеджмента принято выделять различные стратегии финансирования текущих активов в зависимости от отношения менеджера к выбору источников покрытия варьирующей их части, т.е. к выбору относительной величины чистого оборотного капитала. Известны четыре модели поведения: идеальная; агрессивная; консервативная; компромиссная. Выбор той или иной модели стратегии финансирования сводится к установлению величины долгосрочных пассивов и расчёту на её основе величины чистого оборотного капитала как разницы между долгосрочными пассивами и внеоборотными активами (ОК=ДП – ВА). Следовательно, каждой стратегии поведения соответствует своё базовое балансовое уравнение.

Статическое и динамическое представления каждой модели приведены на рис.2.1-рис.2.4. Для удобства введены следующие обозначения: ВА – внеоборотные активы, ТА – текущие активы (ТА=СЧ + ВЧ), СЧ – системная часть текущих активов, ВЧ – варьирующая часть текущих активов, КЗ – краткосрочная кредиторская задолженность, ДЗ - долгосрочный заёмный капитал, СК - собственный капитал, ДП – долгосрочные пассивы (ДП=СК + ДЗ), ОК – чистый оборотный капитал (ОК=ТА – КЗ).

Статическое представление              Динамическое представление

Актив         Пассив                               Активы

В

                                                                                                     Время                                 

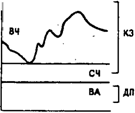
Рис.2.1.Идеальная модель финансового управления оборотными средствами

Построение идеальной модели (рис. 2.1.) основывается на самой сути категорий “текущие активы” и “текущие обязательства” и их взаимном соответствии. Термин “идеальная” в данном случае означает не идеал, к которому нужно стремиться, а лишь сочетание активов и источников их покрытия исходя из их экономического содержания. Модель означает, что текущие активы по велечине совпадают с краткосрочными обязательстввами, т.е. чистый оборотный капитал равен нулю. В реальной жизни такая модель практически не встречается. Кроме того, с позиции ликвидности она наиболее рискованна, поскольку при неблагоприятных условиях (например, необходимо рассчитаться со всеми кредиторами единовременно) предприятие может оказаться перед необходимостью продажи части основных средств для покрытия текущей кредиторсокой задолженности. Суть этой стратегии состоит в том, что долгосрочные пассивы устанавливаются на уровне внеоборотных активов, т.е. базовое балансовое уравнение (модель) будет иметь вид: ДП = ВА.

Для конкретного предприятия наиболее реальна одна из следущих трех моделей стретегии финансового управления оборотными средствами (рис. 2.2, рис.2.3., рис.2.4.), в основу которых положена посылка, что для обеспечения ликвидности как минимум внеоборотные активы и системная часть текущих активов должы покрываться долгосрочными пассивами.

Таким образом, различие между моделями определяется тем, какие источники финансирования выбираются для покрытия варьирующей части текущих активов.

Статистическое представление                 Динамическое представление

Актив         Пассив                                          Активы

                                                                                                                                                                                                                                                                                                                                   Время

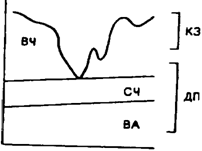
Рис.2.2. Агрессивная модель финансового управления оборотными средствами

Агрессивная модель (рис.2.2.) означает, что долгосрочные пассивы служат источниками покрытия внеоборотных активов и системной части текущих активов, т.е. того их минимума, который необходим для осуществления хозяйственной деятельности. В этом случае чистый оборотный капитал в точности равен этому минимуму (ОК = СЧ). Варьирующая часть текущих активов в полном объёме покрывается краткосрочной кредиторской задолженностью. С позиции ликвидности эта стратегия также весьма рискованна, поскольку в реальной жизни ограничиться лишь минимумом текущих активов невозможно. Базовое балансовое уравнение (модель) будет иметь вид: ДП=ВА + СЧ.

Консервативная модель (рия.2.3.) предполагает, что варьирующая часть текущих активов также покрывается долгосрочными пассивами. В этом случае краткосрочной кредиторской задолженности нет, отсутствует и риск потери ликвидности. Чистый оборотный капитал равен по величине текущим активам (ОК=ТА). Безусловно, модель носит искусственный характер. Эта стратегия предполагает установление долгосрочных пассивов на уровне, задаваемом следующим базовым балансовым уравнением (моделью): ДП=ВА + СЧ + ВЧ.

Статистическое представление                 Динамическое представление

                                                                  Активы

                                                                                  Время

Рис.2.3. Консервативная модель финансового управления оборотными средствами

Компромиссная модель (рис.2.4.) наиболее реальна. В этом случае внеоборотные активы, системная часть текущих активов и приблизительно половина варьирующей части текущих активов покрываются долгосрочными пассивами. Чистый оборотный капитал равен по величине сумме системной части текущих активов и половине их варьирующей части (ОК=СЧ + 0,5ВЧ). В отдельные моменты предприятие может иметь излишние текущие активы, что отрицательно влияет на прибыль, однако это рассматривается как плата за поддержание риска потери ликвидности на должном уровне. Стратегия предполагает установление долгосрочных пассивов на уровне, задаваемом следующим базовым балансовым уравнением (моделью): ДП=ВА + СЧ + 0,5ВЧ

Статистическое представление                 Динамическое представление

                                                             Активы

                                                                            Время

Рис.2.4.Компромиссная модель финансового управления оборотными средствами

Пример

Рассчитать различные варианты стратегии финансового управления оборотными средствами (рис.2.5.) по табл. 2.1.

Таблица 2.1.

Янв.  Фев.   Март   Апр.  Май  Июн. Июл. Авг. Сент. Окт. Нояб.  Дек.

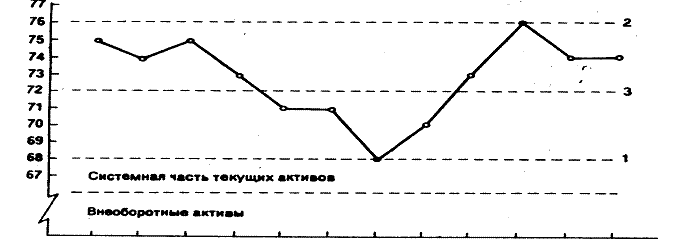
 Рис. 2.5.  Различные стратегии финансирования

Комментарий к расчётам

1.      Системная часть текущих активов представляет собой минимальную потребность в оборотных средствах и равна 8 млн. руб. (по данным июля).

2.      Минимальная потребность в источниках средств равна 68 млн. руб. в июне, максимальная - 76 млн. руб. в октябре.

3.      Линия 1 характеризует агрессивную стратегию, при которой долгосрочные пассивы покрывают внеоборотные активы и системную часть текущих активов. В соответствии с этой стратегией предприятия его долгосрочные пассивы должны составить 68 млн. руб. (68-60).

4.      Линия 2 характеризует консервативную стратегию, в соответствии с которой долгосрочные пассивы поддерживаются на максимально необходимом уровне, т.е. в размере 76 млн. руб. В этом случае чистый оборотный капитал составит 16 млн. руб. (76- 60).

5. Линия 3 характеризует компромиссную стратегию, согласно которой долгосрочные пассивы устанавливаются в размере, покрывающем внеоборотные активы, системную часть текущих активов и половину прогнозного значения варьирующей части текущих активов, т.е. в размере 72 млн. руб. В этом случае частный оборотный капитал составит 12 млн. руб. (72- 60).