Расчет аннуитетов

Аннуитеты представляют собой наиболее сложные алгоритмы начисления процента — предварительным (пренумерандо) или последующим (постнумерандо).

1. При расчете будущей стоимости аннуитета на условиях предварительных платежей (пренумерандо) используется следующая формула:

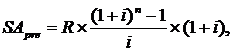
где SApre — будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо);

R— член аннуитета, характеризующий размер отдельного платежа;

i— используемая процентная ставка, выраженная десятичной дробью;

п— количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать будущую стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), при следующих данных: период платежей по аннуитету предусмотрен в количестве 5 лет; интервал платежей по аннуитету составляет один год (платежи вносятся в начале года);сумма каждого отдельного платежа (члена аннуитета) составляет 1000 усл. ден. eд.; используемая для наращения стоимости процентная ставка составляет 10% в год (0,1).

Подставляя эти значения в приведенную формулу, получим:

будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), равна:

  2. При расчете будущей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется следующая формула:

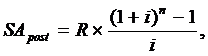
где  SApost — будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо);

         R— член аннуитета, характеризующий размер отдельного платежа;

         i — используемая процентная ставка, выраженная десятичной дробью;

         п — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать будущую стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), по данным, изложенным в предыдущем примере (при условии взноса платежей в конце года).

Подставляя эти данные в приведенную формулу, получим:

будущая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), равна:

Сопоставление результатов расчета по двум примерам показывает, что будущая стоимость аннуитета, осуществляемого на условиях предварительных платежей, существенно превышает будущую стоимость аннуитета, осуществляемого на условиях последующих платежей, т.е. в первом случае плательщику обеспечена гораздо большая сумма дохода.

3. При расчете настоящей стоимости аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), используется следующая формула:

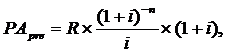
где РАpre— настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо);

        R — член аннуитета, характеризующий размер отдельного платежа;

         i — используемая процентная (дисконтная) ставка, выраженная десятичной дробью;

         п — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

Пример: Необходимо рассчитать настоящую стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), при следующих данных:

период платежей по аннуитету предусмотрен в количестве 5 лет;

интервал платежей по аннуитету составляет один год (при внесении платежей в начале года);

сумма каждого отдельного платежа (члена аннуитета) составляет 1000 усл. ден. eд.;

используемая для дисконтирования стоимости ставка процента (дисконтная ставка) составляет 10% в год (0,1).

Подставляя эти значения в приведенную формулу, получим:

настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей (пренумерандо), равна:

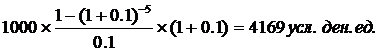
4. При расчете настоящей стоимости аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), применяется следующая формула:

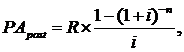
где PApost— настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо);

         R— член аннуитета, характеризующий размер отдельного платежа;

         i — используемая процентная (дисконтная) ставка, выраженная десятичной дробью;

         п — количество интервалов, по которым осуществляется каждый платеж, в общем обусловленном периоде времени.

   Пример: Необходимо рассчитать настоящую стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), по данным, изложенным в предыдущем примере (при условии взноса платежей в конце года).

  Подставляя эти данные в приведенную формулу, получим:

настоящая стоимость аннуитета, осуществляемого на условиях последующих платежей (постнумерандо), равна:

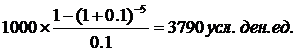
Сопоставление результатов расчета по двум последним примерам показывает, что настоящая стоимость аннуитета, осуществляемого на условиях предварительных платежей, существенно превышает настоящую стоимость аннуитета, осуществляемого на условиях последующих платежей, т.е. в первом случае в процессе дисконтирования плательщику гарантирована гораздо большая сумма дохода в настоящей стоимости,

5. При расчете размера отдельного платежа при заданной будущей стоимости аннуитета используется следующая формула:

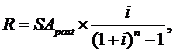
где R— размер отдельного платежа по аннуитету (член аннуитета при предопределенной будущей его стоимости); 

         SApost — будущая стоимость аннуитета (осуществляемого на условиях последующих платежей);

         i — используемая процентная ставка, выраженная десятичной дробью;

         п — количество интервалов, по которым намечается осуществлять каждый платеж, в обусловленном периоде времени.

6. При расчете размера отдельного платежа при заданной текущей стоимости аннуитета используется такая формула:

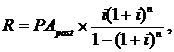
где R — размер отдельного платежа по аннуитету (член аннуитета при известной текущей его стоимости);

        PApost— настоящая стоимость аннуитета (осуществляемого на условиях последующих платежей);

        i— используемая процентная ставка, выраженная десятичной дробью;

        п — количество интервалов, по которым намечается осуществлять каждый платеж, в обусловленном периоде времени.

В процессе расчета аннуитета возможно использование упрощенных формул, основу которых составляет только член аннуитета (размер отдельного платежа) и соответствующий стандартный множитель (коэффициент) его наращения или дисконтирования.

В этом случае формула для определения будущей стоимости аннуитета (осуществляемого на условиях последующих платежей), имеет вид:

SApost = R × lA,

где SApost— будущая стоимость аннуитета (осуществляемого на условиях последующих платежей);

          R — член аннуитета, характеризующий размер отдельного платежа;

          lA — множитель наращения стоимости аннуитета, определяемый по специальным таблицам, о учетом принятой процентной ставки и количества интервалов в периоде платежей.

       Соответственно, формула для определения настоящей стоимости аннуитета имеет вид:

PApost = R × DA,

где PApost— настоящая стоимость аннуитета (осуществляемого на условиях последующих платежей);

        R — член аннуитета, характеризующий размер отдельного платежа;

        DA — дисконтный множитель аннуитета, определяемый по специальным таблицам, с учетом принятой процентной (дисконтной) ставки и количества интервалов в периоде платежей.

Использование стандартных множителей (коэффициентов) наращения и дисконтирования стоимости существенно ускоряет и облегчает процесс оценки стоимости денег во времени.