Для необратимых круговых процессов выполняется неравенство Клаузиуса, а для обратимых круговых процессов выполняется равенство Клаузиуса: «Приведённое кол-во теплоты, полученное системой при любом квазистатическом круговом процессе, равно нулю».
Энтропия: Энтропия системы есть функция её состояния, определённая с точностью до произвольной постоянной. Разность энтропии в двух равновесных состояниях 2 и 1, по определению, равна приведённому кол-ву теплоты, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути.
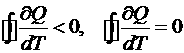
– полный дифференциал 
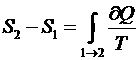, где 1 – необратимый процесс, а 2 – обратимый
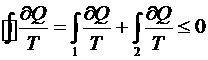
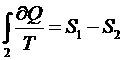, т.к. процесс 2 – квазистатический.
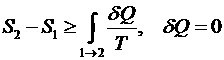, т.к. процесс – адиабатический
Закон возрастания энтропии: энтропия адиабатически изолированной системы не может убывать; она либо возрастает, либо остаётся постоянной.
Энтропия – аддитивная функция состояния. При расширении в пустоту энтропия увеличивается. Энтропия максимальна в состоянии равновесия.
Энтропия 
определяется логарифмом числа микросостояний, посредством которых реализуется рассматриваемое макросостояние:
– формула Больцмана.
Термодинамические потенциалы.
.
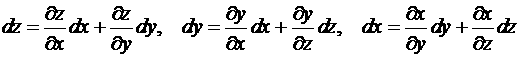
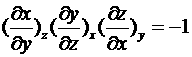Если 
, то
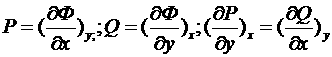
– термодинамическое тождество.
Энтальпия: 
Энтропия:
Свободная энергия: 
Т/Д функция Гиббса: 
Поможем написать любую работу на аналогичную тему