Электрическим диполем называется пара точечных зарядов разного знака, одинаковых по модулю, жестко закрепленных на одинаковом расстоянии друг от друга. Суммарный заряд диполя равен нулю.
Для характеристики диполя вводят понятие дипольного момента (
). Проведем вектор из отрицательного заряда в положительный. Тогда дипольным моментом называется вектор 
. 
.
Рассчитаем поле диполя.
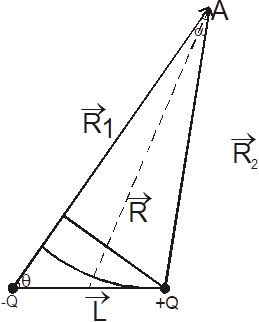
Наша задача найти поле в точке 
.
Это можно сделать двумя способами:
1) из принципа суперпозиции;
2) используя свойство аддитивности работы.
Если есть два поля и тело перемещать , то можно найти работу сил первого поля и работу сил второго поля по перемещению этого тела.
Потенциал точки относительно бесконечности – это работа сил поля при перемещении единичного положительного заряда из точки в бесконечность по любой траектории.
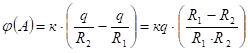
Представим, что 
. Запишем потенциал в точке для данного приближения. Тогда 
, а дуга окружности переходит в перпендикуляр, поэтому 
.
.
Потенциал поля точечного заряда на больших расстояниях убывает пропорционально первой степени расстояния, а потенциал поля диполя – пропорционально второй степени.
.
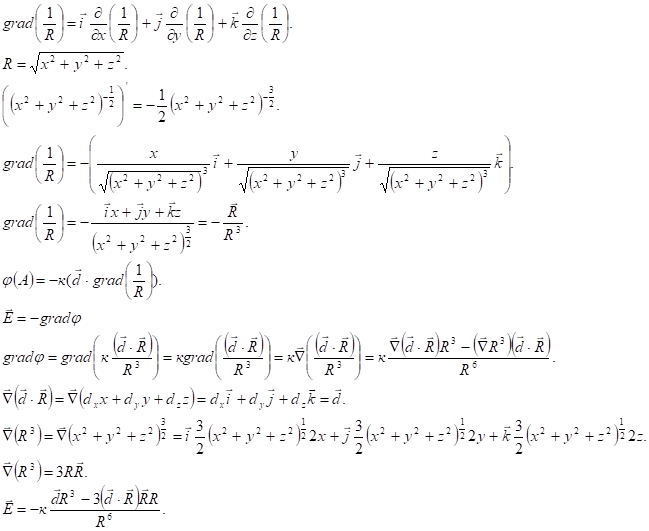
- единичный вектор в направлении точки из диполя.
.
Поле диполя убывает пропорционально третьей степени расстояния.
Пример 1.
.
Пример 2.
Поможем написать любую работу на аналогичную тему