Если записать закон Ома в дифференциальной форме в некоторой точке 
, то в общем случае функция 
имеет довольно сложный вид.
I. Будем считать вектор коллинеарным с вектором 
, тогда 
. Разложим функцию 
в ряд Тейлора в близи нуля, считая, что мало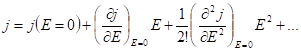 
Пусть рассматриваемый нами материал не сверхпроводник, тогда слагаемое 
. Введем следующие обозначения 
, 
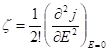, тогда для не сверхпроводника имеет быть место равенство 
Числа 
и 
для каждого проводника свои, но их можно измерить. - линейная проводимость, - квадратичная проводимость.
Если 
, то проводник линейный. Если и сравнимы, то проводник нелинейный.
Для линейного проводника закон Ома в дифференциальной форме выглядит следующим образом 
.
II. Рассмотрим проводимость анизотропных сред (кристаллы).
.
Возьмем какой-нибудь кристалл и померим его проводимость в разных направлениях:
Подключим прибор последовательно и померим проводимость между гранями, перпендикулярными 
, 
, 
. Полученные значения будут не обязательно одинаковы.
Померим проводимость в направлении телесной диагонали, 
- компоненты одинаковы. В таком случае компоненты регистрируемого тока можно записать следующим образом: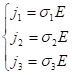 
Поскольку 
то 
, значит ток потечет не в направлении вектора 
, а в сторону.
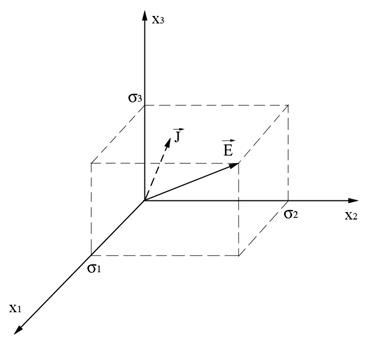Запишем закон Ома в случае, когда вектор неколлинеарный с вектором .
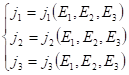
разложим 
в ряд Тейлора в близи нуля как функцию трех переменных:
Пусть мы исследуем не сверхпроводник, и нет токов при отсутствии полей, тогда слагаемые 
равны нулю.
Введем обозначения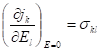 
и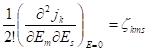 
, тогда 
- тензор линейной проводимости (тензор II ранга)
- тензор нелинейной проводимости (тензор III ранга)
Если проводник линейный 
, то закон Ома для анизотропной среды имеет вид: 
.
Поможем написать любую работу на аналогичную тему