Разрядка конденсатора
Пусть у нас есть конденсатор емкостью ![]() на котором заряд
на котором заряд ![]() .
.
Соберем цепь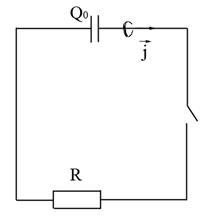
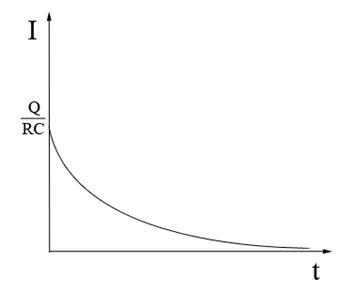
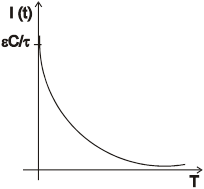
И посмотрим как будет меняться сила тока ![]() от времени.
от времени.
Выберем сечение проводника и посмотрим, как соотносятся заряд на конденсаторе и заряд, который проходит через данное сечение в единицу времени (сила тока). Сколько протекло заряда в единицу времени, на столько же и уменьшился заряд на конденсаторе: ![]()
![]()
![]() .
.
Знак минус, потому что убыль заряда на конденсаторе.
Запишем соотношение между емкостью ![]() и разностью потенциалов
и разностью потенциалов ![]() :
: ![]() . Теперь запишем закон Ома, таким образом свяжем ток в проводнике и разность потенциалов:
. Теперь запишем закон Ома, таким образом свяжем ток в проводнике и разность потенциалов: ![]() .
.
Теперь решим дифференциальное уравнение: ![]()
![]()
![]()
![]() .
.
При ![]()
![]() , значит
, значит ![]() ,
, ![]() .
.
Величина ![]() - постоянная времени. Предположим, что в данный момент времени ток во всех точках цепи одинаков – такие токи называются квазистационарными.
- постоянная времени. Предположим, что в данный момент времени ток во всех точках цепи одинаков – такие токи называются квазистационарными.
Зарядка конденсатора.
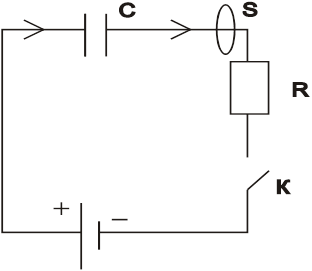
Считаем, что процессы квазистационарны, то есть настолько медленны, что в данный момент времени в любой точке цепи токи одинаковы. Полный заряд в единицу времени через площадку ![]() – ток.
– ток.
Сколько прошло заряда через поверхность, столько же заряда получил конденсатор.
![]() .
.
Запишем закон Кирхгофа:
![]() .
.
![]() можно записать, зная емкость конденсатора и его заряд в данный момент времени.
можно записать, зная емкость конденсатора и его заряд в данный момент времени.
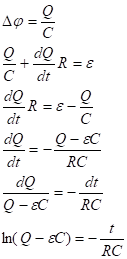
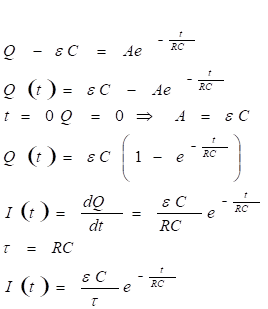
Поможем написать любую работу на аналогичную тему

