Рассмотрим движение частицы в некотором однородном поле. Будем задавать его (поле) не силами а потенциальной энергией (т.е. силы консервативны). Пусть диссипативных сил нет. Рассмотрим следующий вид зависимости потенциальной энергии от координаты.
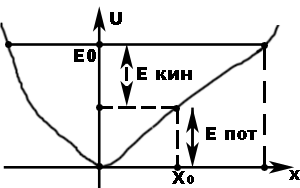
Пусть минимум потенциальной энергии в точке (0,0). Такое поле – потенциальная яма.
Пусть в некоторый момент времени, когда точка была в нуле, телу сообщили кинетическую энергию 
, т.к. нет диссипативных сил, то полная механическая энергия постоянна и равна . В точке 
, частица имеет потенциальную энергию, определяющейся точкой на графике. При движении по оси 
будет расти потенциальная энергия и уменьшаться кинетическая, и в некоторой точке 
потенциальная энергия станет равна а кинетическая станет равна нулю.
Частица совершает непрерывные движения в ограниченной области пространства повторяя свою траекторию – это колебательное движение.
Пусть колебания малые. Разложим 
в ряд Тейлора вблизи ноля:
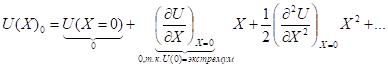
Допустим, что колебания настолько малы, что мы с достаточной погрешностью можем ограничиться квадратичным слагаемым. Тогда:
, где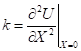 
.
Т.о. если энергия мала, то низ ямы можно представить как параболу.
;
;
;
.
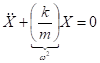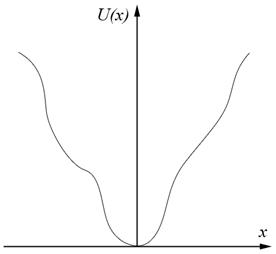
Мы рассмотрели как описывать механические движения в потенциальной яме. Если колебания на столько маленькие, что «дно ямы» можно описать параболой, то колебания описываются формулой 
, аналогично могут описываться и большие колебания, при условии, что яма параболическая.
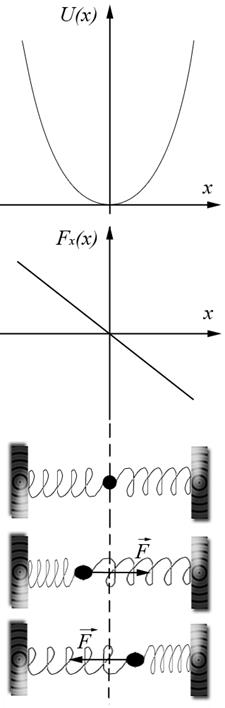
Рассмотрим параболическую яму или самое донышко любой другой.
Итак, зависимость потенциальной энергии тела от координаты имеет вид 
. Найдем зависимость силы, действующей на тело, от его координаты: 
. Заметим, что эта сила линейна.
Решим дифференциальное уравнение , описывающее движение в параболической яме.
, 
- в общем случае произвольные комплексные числа. Поскольку 
- действительная величина, то всегда выполняется соотношение 
, а значит 
это тождество верно для любого момента времени 
.
Если 
, 
.
Пусть 
, 
, где 
- некоторые произвольные действительные числа.
Запишем решения в другом виде 
.
Запишем комплексные числа в тригонометрическом виде 
распишем косинус суммы 
, где 
, 
.
Все, что колеблется по такому закону называется «гармонические колебания» 
Величина 
называется амплитудой гармонических колебаний,
- фаза гармонических колебаний – величина, зависящая от времени. 
- начальная фаза.
Если координата записывается , то скорость и ускорение записываются соответственно
, 
.
Найдем такое время 
, через которое 
повторится, т.е. выполняется равенство 
. 
, 
, 
, где 
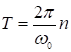величина называется периодом колебаний. Периодов много, но можно рассматривать наименьший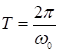 
.
- круговая (циклическая) частота колебаний 
.
- называется «просто» частота колебаний. 
.
Напишем выражения для энергий:
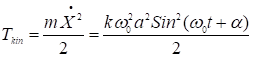
Энергия осциллирует и всегда положительна.
.
Полная энергия не зависит от времени – сохраняется.
- произвольные постоянные в общем решении дифференциального уравнения, их можно найти из начальных условий.
Н.р. 
,
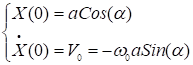решив эту систему, найдем , зная 
и 
,
, 
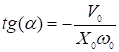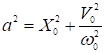
Поможем написать любую работу на аналогичную тему