В 60-х годах прошлого века (около 1860 г.) Максвелл, основываясь на идеях Фарадея, обобщил законы электростатики и электромагнетизма: теорему Гаусса – Остроградского для электростатического поля 
и для магнитного поля 
; закон полного тока 
; закон электромагнитной индукции 
, и в результате разработал законченную теорию электромагнитного поля.
Теория Максвелла явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения понять широкий крут явлений, начиная от электростатического поля неподвижных зарядов и заканчивая электромагнитной природой света.
Математическим выражением теории Максвелла служат четыре уравнения Максвелла. которые принято записывать в двух формах: интегральной и дифференциальной. Дифференциальные уравнения получаются из интегральных с помощью двух теорем векторного анализа – теоремы Гаусса и теоремы Стокса. Теорема Гаусса:
(1)
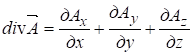(2)
-
проекции вектора 
на оси; V - объем, ограниченный поверхностью S.
Теорема Стокса: 
. (3)
здесь rot -
ротор вектора , который является вектором и выражается в декартовых координатах следующим образом: 
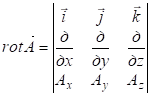, (4)
S - площадь, ограниченная контуром L.
Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей.
Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности зарядов и токов в каждой точке этого поля.
Поможем написать любую работу на аналогичную тему