Ток смещения. Второе уравнение Максвелла - Лекции по физике. Электричество.

Максвелл обобщил закон полного тока  предположив, что переменное электрическое поле, также как и электрический ток, является источником магнитного поля. Для количественной характеристики "магнитного действия" переменного электрического поля Максвелл ввел понятие тока смещения.

По теореме Гаусса - Остроградского поток электрического смещения сквозь замкнутую поверхность                                           

Продифференцировав это выражение по времени, получим для неподвижной и недеформирусмой поверхности S 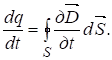                                                        (8)

Левая часть этой формулы имеет размерность тока, который, как известно, выражается через вектор плотности тока                .                                     (9)

Из сравнения (8) и (9) следует, что  имеет размерность плотности тока: А /м2. Максвелл предложил назвать  плотностью тока смещения:

                                                                 .                                      (10)

Ток смещения 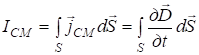                              .                         (11)

Из всех физических свойств, присущих действительному току (току проводимости), связанному с переносом зарядов, ток смещения обладает лишь одним: способностью создавать магнитное поле. При "протекании" тока смещения в вакууме или диэлектрике не выделяется тепло. Примером тока смещения может служить переменный ток через конденсатор. В общем случае токи проводимости и смещения не разделены в пространстве и можно говорить о полном токе, равном сумме токов проводимости и смещения:                                                                                    (12)

С учетом этого Максвелл обобщил закон полного тока, добавив в правую часть его ток смещения 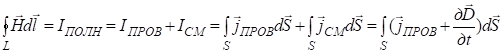.           (13)                                                                                        

Итак, второе уравнение Максвелла в интегральной форме имеет вид:

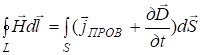                                                       .                                            (14)

Из (3) следует, что                                .                                             (15)

Из сравнения (14) и (15) находим, что 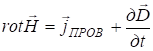                   .                 (16)

Это и есть второе уравнение Максвелла в дифференциальной форме.