Чем замечательна пустота? В пустоте нет зарядов 
, 
. Уравнения приобретают вид:
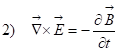
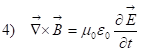
Ну, и сразу бросается в глаза замечательная симметрия, симметрия нарушается только тем, что в уравнении 4) константа размерная и знак. Размерная константа – несущественно, это связано с системой единиц, можно выбрать такую систему единиц, где эта константа просто единицей будет. Это дифференциальные уравнения, но положение осложняется тем, что переменные перекрещиваются. Поставим для начала скромную задачу – написать уравнение, которое содержало бы только одну неизвестную величину, 
например.
Значит, первая наша цель – исключить из уравнения 2) 
. Как исключит? А очень просто: мы видим, что в четвёртом уравнении сидит переменная , если мы на это уравнение подействуем векторно оператором 
, то в правой части выскочит 
…
Второе уравнение даёт: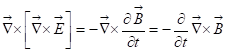 
. Добавляя четвёртое уравнение мы получаем: 
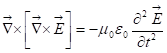или
.
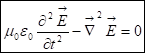Мы получили уравнение, которое утверждает, что вторая производная по времени от связана со вторыми производными от компонент по координатам, то есть изменение величины в данной точке со временем увязано с пространственным изменением этой величины.
Поможем написать любую работу на аналогичную тему