Напряженность поля.

Будем считать, что заряд создает вокруг себя в пространстве электрическое поле. Это поле обнаруживается при внесении в него других зарядов из-за действия на них силы Кулона. Рассмотрим действие заряда  на , разделив его на два этапа:

1. 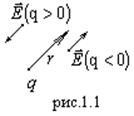Точечный заряд  создает в пространстве электрическое поле, напряженность которого:

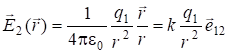,                            (1.4)

где  - радиус - вектор точки определения поля,  - орт, направленный от заряда при .

2.     Точечный заряд , находящийся в точке измерения, испытывает действие силы:

.                                           (1.5)

В таком случае, напряженность поля в точке - это величина, равная силе, испытываемой единичным пробным зарядом, помещенным в эту точку, со стороны поля.

Единицы измерений в СИ: F- Ньютон, q - Кулон, Е - В/м.

На основании (1.5) определение механической силы, действующей на заряд, сводится к определению поля , в котором находится заряд. F, E, q –определяются в одной точке (локально). Принцип суперпозиции применим для .  Для системы зарядов:

.

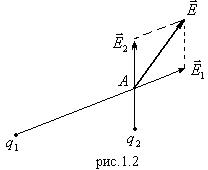
Напряженность поля любого числа точечных зарядов равна сумме напряженностей полей каждого точечного заряда.

При непрерывном распределении заряда по объему тела принцип суперпозиции можно записать в виде рис.1.2

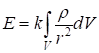,                           (1.6)

где  - полный заряд тела объема V, - объемная плотность заряда.

Примеры.

1. 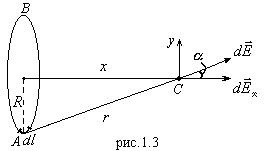       Вычислить напряженность поля на оси тонкого равномерно заряженного зарядом q кольца радиуса R.

Выберем элементарный заряд, распределенный на длине :

.

Напряженность поля от этого элементарного заряда:

.

Из рис.1.3 видно, что имеются две проекции  ‑  и :

;           ,

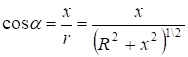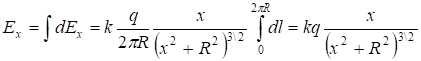,           (1.7)

,

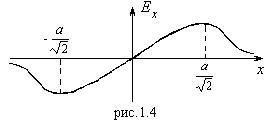так как для каждой точки А имеется симметричная точка В, заряд в которой создает противоположно направленную относительно у проекцию напряженности поля. При х>>R,  - т.е. совпадает с полем точечного заряда. Зависимость  представлена на рис.1.4.

2. 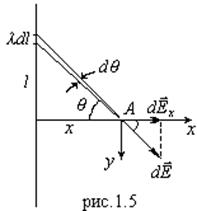       Найти поле равномерно заряженной прямой бесконечной нити. Линейный заряд нити .

Выберем элементарный заряд , распределенный на длине :

;

Напряженность поля, создаваемая этим зарядом в точке А, . Имеются две проекции  (см. рис.1.5) -  и :

.                              (1.8)

Так как       , то       ;     . Подставим  и  в формулу (1.8); учтем вторую половину нити и получим:

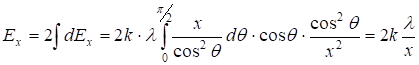.           (1.9)

 в силу симметрии задачи.