Потенциальность электростатического поля.

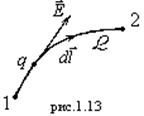
          При перемещении на  заряда  в поле напряженности  совершается работа:

Видно, что работа, совершаемая полем, положительна, если q>0. При перемещении заряда из точки 1 в точку 2 по траектории L  рис.1.13 работа равна:

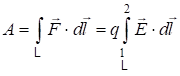.                              (1.26)

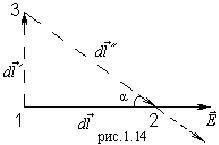
Разобьём путь от 1 к 2 на участки, показанные на рис.1.14. На участке 12 работа:

.

На участках 13 и 32:

.

Видно, что работа по перемещению заряда в электрическом поле  не зависит от траектории, а зависит лишь от начальной и конечной точек пути. Такое поле называется потенциальным. Легко показать, что работа при перемещении заряда  в поле  по замкнутому контуру равна нулю.

                       -                  (1.27)

циркуляция  по замкнутому контуру  равна нулю. Это другое (эквивалентное) определение потенциальности .

          В дифференциальной форме можно записать:

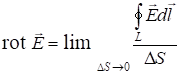.                                                   (1.28)

Через векторный оператор ,  введенный в (1.18),  это:

,                                     (1.29)

где

.

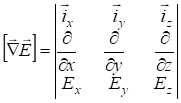Таким образом, дифференциальная формулировка потенциальности электростатического поля :

.                                   (1.30)

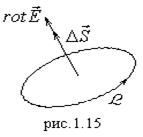
                Из определения ясно, что  - это вектор (рис.1.15). Знак его и направление обхода контура , площадь которого , связаны правилом буравчика. Можно связать циркуляцию вектора по контуру, ограничивающему поверхность, с потоком его ротора через эту поверхность. Из определения (1.28) видно, что:

     -                            (1.31)

это формула Стокса. Поток вектора  через поверхность, ограниченную контуром , равен циркуляции вектора  по этому контуру.