Электродинамика – это динамика электрических явлений. В основе лежит закон Кулона, он опирается на том, что существует электрические заряды различных знаков, а также, что одноимённые отталкиваются, разноимённые притягиваются. Величина заряда определяет интенсивность взаимодействия. Сам закон имеет вид:
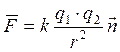, где 
Можно использовать эту формулу для определения величины заряда.
Коэффициент k-зависит от выбора систем единиц. Но мы задачи будем решать в системе единиц СИ, в которой выберем 
, 
Ф/м.
Если два одинаковых заряда находятся на расстоянии 1 метра и сила взаимодействия между ними равна 
, то величина каждого заряда равняется 1 Кл.
Мы часто имеем дело с непрерывно распределённым зарядом и если в элементе объёма dV сосредоточен заряд dq, то заряд в единице объёма в каждой точке называется плотностью заряда 
. И если известно пространственное распределение заряда можно определить величину заряда в элементе объёма dV: dq=
dV. Если заряд распределён по поверхности, можно ввести поверхностную плотность заряда: 
. dq – заряд расположенный на площадочке dS. Аналогично можно ввести линейную плотность заряда 
Когда мы имеем дело с движущимися зарядами, физический смысл имеет понятие силы тока. Сила тока – это количество электричества, проходящего через полное поперечное сечение проводника в единицу времени. Часто мы встречаемся со случаем, когда ток не равномерно распределён по сечению. И вообще, величина тока через сечение различна в разных элементах тока этого сечения и зависит от положения этого элемента сечения относительно тока. В этом случае вводится понятие плотности тока
,
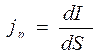-величина тока проходящего через площадку dS, а 
- плотность тока – это сила тока, проходящего через сечение dS, вдоль направлению нормали к этой площадке. Естественно, что если 
располагается в плоскости площадки, то 
Важнейшим закон в электродинамике является закон сохранения заряда или в дифференциальной форме он называется – уравнение непрерывности. Пусть в некотором объёме dV имеется заряд q.
-dq/dt –есть убыль заряда в единицу времени;
dS – элемент поверхности, в которой заключён заряд;
jdS – заряд, проходящий через dS в единицу времени;
Закон сохранения заряда (для незамкнутой системы) можно сформулировать так – убыль заряда в единицу времени в объёме dV равен величине заряда, вытекающего через поверхность этого объёма в единицу времени. Но, так как 
, то закон сохранения заряда запишется в такой форме:
После небольших преобразований (в правой части используем теорему Гаусса-Остроградского, а в левой части меняем операции дифференцирования и интегрирования) - мы заменили полную производную на частную, здесь постоянном объёме, получаем
- заряд, протекающий через S.
Выведем этот закон в дифференциальной форме. Запишем формулу полного заряда . Возьмём производную по времени, получим: 
Физический смысл – в точках, в которых меняется со временем, имеются истоки тока j.
Поможем написать любую работу на аналогичную тему