Воспользуемся теоремой Грина: 
произвольные скалярные функции. Они имеют производные и не обращаются в 
в любой точке. Положим, что 
и 
. Теперь подставим в формулу Грина, получим: 
.
Пусть заряды распределены в замкнутой поверхности S . Поскольку функции 
не должны обращаться в бесконечность не в какой точке. а потенциал, в частности точечного заряда 
, то мы исключим точки в которых 
обращается в 0. Выберем эту точку бесконечно малой замкнутой поверхностью. И объём, по которому будет вестись интегрирование, будет заключаться между внешней и внутренней поверхностью (рисун)
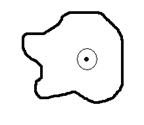
Здесь дана некоторая точка, где r = 0. Мы должны исключить интегрирование по внешней поверхности и исключить данную точку. Мы сделаем это следующим образом – мы эту точку окружим, а затем радиус устремим к нулю и выкинем выбранную точку. Поэтому, интеграл по замкнутой поверхности распадается на внешний и внутренний.
, 
(внешнюю поверхность устремляем в бесконечность). Заметим, что здесь такие зависимости: 
, а следовательно, этот интеграл стремится к нулю, то есть он пропадает, когда мы охватываем всё пространство. Теперь рассмотрим интеграл по внутренней поверхности. 
=(по теореме о среднем)=
, при r 
, интеграл . Значит,
=
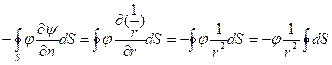(по теореме о среднем) =
. При r видно, 
в данной точке, что 
. Мы получаем: 
это потенциал поля системы зарядов в единице объёма. Это решение уравнение Пуассона.
Рассмотрим потенциал поля заряда на большом расстоянии. Здесь 
dV 
, 
r 
R Теперь вынесем R из под корня и подставим в уравнение.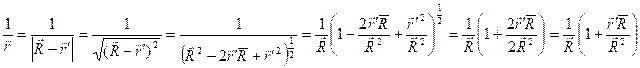 
, 
- дипольный момент зависит только от распределения заряда в этом объёме.
На больших расстояниях поле определяется только дипольным моментом 
Для простоты рассмотрим набор дискретных зарядов: 
. Здесь 
, а 
Тогда запишем следующий интеграл: 
. Вынесем за скобки сумму зарядов и сделаем преобразования: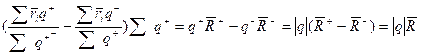 
Мы получили радиус вектор положительных зарядов.
- дипольный момент, и направлен он от минуса к плюсу.
Дипольный момент определяет поле нейтральной системы зарядов на больших расстояниях. РОЛЬ дипольного момента: поле нейтральной системы зарядов определяется её дипольным моментом!
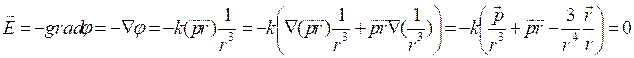
Найдём напряжённость диполя:
- поле диполя.
Поможем написать любую работу на аналогичную тему