Уравнения электромагнитного поля как обобщение опытных фактов.

Начнём с фундаментального опытного закона Кулона

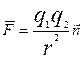, где де .  Напряжённость электрического поля будет равна 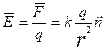. Здесь  - источник поля.

Запишем этот закон в интегральной форме. Пусть заряд q создаёт электрическое поле. Окружим этот заряд некой замкнутой поверхностью S. Выберем на этой поверхности элемент dS. n – нормаль к dS. Нормаль обычно строится наружу от объёма. Начнём поток вектора напряжённости через эту поверхность.

Здесь -элемент телесного угла – это проекция вектора площади(нормали к её поверхности) на направление E. Если внутри будет не один заряд, а много, то в следствии принципа суперпозиции , и окончательно получаем поток вектора напряженности E через произвольную замкнутую поверхность равен сумме зарядов внутри этой поверхности. Если заряд внутри объёма распределён непрерывно, то

К левой части применим теорему Остроградского-Гаусса, откуда получаем . Отсюда в свою очередь следует .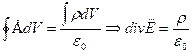

Физический смысл: в тех точках где имеется заряд  дивергенция  не равняется 0, имеется источник поля.

Найдём уравнение для магнитного поля. Используем для этого опытный закон. для магнитной индукции бесконечно длинного провода по которому течёт ток I. r-расстояние от провода до точки наблюдения

 Перепишем его в форме или в более общей форме . Окончательно закон БСЛ в интегральной форме примет  вид

Физический смысл: Циркуляция вектора  по произвольному замкнутому контуру равняется сумме токов, которые охватывают этот контур.

Выразим этот закон в дифференциальной форме. Возьмём контур, охватывающий ток, считая, что у нас ток нелинейный, а  не прерывный. Плотность тока -  , то ток, который охватывается этим контуром или тоже самое, проходит через поверхность, которая опирается на данный контур будет равен  , а следовательно, наш закон примет вид .

К левой части применим теорему Стокса и получим:

 И получаем, что

так как  произвольное направление, мы можем выбрать направление по оси вдоль (x,y,z), окончательно получаем закон Био-Савара-Лапласа в дифференциальной форме  Смысл: В точках, где имеется ток, существует завихрённость магнитного поля. Однако, этот закон верен только для постоянного тока. Покажем это. Возьмём от обеих частей этого уравнения дивергенцию.

Так как , то , а из уравнения непрерывности (закона сохранения заряда)  следует, что , а следовательно, что  и =const. Для того чтобы закон сохранения заряда выполнялся даже для случая нестационарного в дифференциальное уравнение для магнитного поля, Максвелл добавил ещё один член  и уравнение принимает вид

 Здесь   =.

Физический смысл: вихревое магнитное поле создаётся токами проводимости переменным электрическим полем.