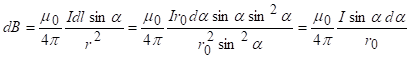Закон Био - Савара - Лапласа - Лекции по электростатике

Био, Савар и Лаплас установили закон, который позволяет вычислить магнитную ин дукцию поля, созданного элементом тока Id на расстоянии  от него:

        dB = ,                                                         (5)

т.е. индукция магнитного поля, создаваемого элементом тока Id точке А, (см. рис. 3), на расстоянии r от него, пропорциональна величине элемента тока и синусу угла a, равного углу между направлениями элемента тока Id и , а также обратно пропорциональна квадрату расстояния между ними;

Закон Био - Савара - Лапласа в векторной форме имеет вид:   d=.         (6)

Закон Био - Савара - Лапласа позволяет вычислить магнитную индукцию поля любых систем токов, используя принцип суперпозиции магнитных поля   = .        (7)

Применим закон Био - Савара - Лапласа и принцип суперпозиции (7) к расчету магнит ных полей следующих токов:

1. Поле поямого тока:

α1 Внимание! Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы. Расчет стоимостиГарантииОтзывы   a2                   . α                            rda α                                            I                                                                          Рис. 4

Из рис. 4 с учетом (6) находим, что d плоскости, в которой лежат d и ; далее можно найти  ,откуда, принимая во внимание, что  получаем . С учетом этого из (5) находим: интегрируя последнее равенство, получаем:

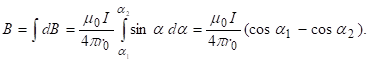                                                                 (8)

Для бесконечно длинного проводника ,  и  из  (8) следует, что

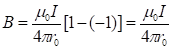                                                                                                            (9)

C учетом (4) и (9) cила взаимодействия двух бесконечно длинных тонких и параллельных проводников          .                             (10)

Пусть I1 = I2 = I,  r0 = 1м,  l = 1м,  F = Н, тогда I = 1 А. Это было строгое определение единицы силы тока - ампера.

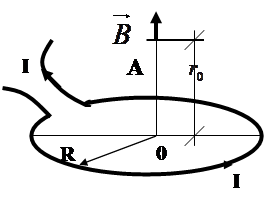2. Поле кругового тока

Можно показать, что магнитная индукция поля, созданного круговым током радиуса R, на расстоянии r0 вдоль перпендикуляра, восстановленного из центра контура,  (см. рис.5), будет 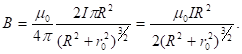                 (11)

                                                           В частности, в центре кругового тока ,

Для плоской катушки, состоящей из N, витков магнитная индукция на оси катушки

                                                                    .                                                       (13)

При больших расстояниях от контура, (рис. 5), т. е. при r0 >> R из (11) получим

                                                                                                                           (14)