 1) Сфера. Найдем напряженность сферы внутри E1
и снаружи E2. Выбираем в качестве гауссовой поверхности сферу радиусом r<R для нахождения поля внутри и r>R – снаружи сферы.
1) Сфера. Найдем напряженность сферы внутри E1
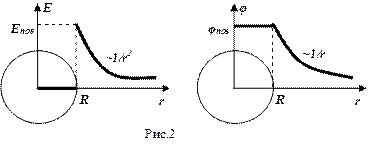
и снаружи E2. Выбираем в качестве гауссовой поверхности сферу радиусом r<R для нахождения поля внутри и r>R – снаружи сферы. ![]() , так как у сферы (рис.2) заряды расположены только на поверхности, поэтому напряженность поля внутри сферы равна нулю (нет зарядов), а потенциал постоянен и равен потенциалу на поверхности.
, так как у сферы (рис.2) заряды расположены только на поверхности, поэтому напряженность поля внутри сферы равна нулю (нет зарядов), а потенциал постоянен и равен потенциалу на поверхности. ![]() , то есть, на расстояниях r>R от своего центра сфера ведет себя как точечный заряд. Ее напряженность равна
, то есть, на расстояниях r>R от своего центра сфера ведет себя как точечный заряд. Ее напряженность равна ![]() (2), а потенциал равен
(2), а потенциал равен ![]() (3). Напряженность и потенциал на поверхности сферы, соответственно, равны
(3). Напряженность и потенциал на поверхности сферы, соответственно, равны ![]() (2*) и
(2*) и ![]() (3*).
(3*).
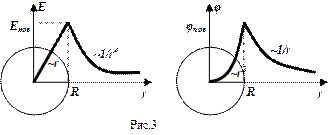 2) Объемно заряженный шар при r>R ведет себя также как и сфера и для него справедливы выражения (2,2*) и (3, 3*). В отличии от сферы внутри шара есть заряды, а значит напряженность поля отлична от нуля и потенциал не постоянен (рис.3).
2) Объемно заряженный шар при r>R ведет себя также как и сфера и для него справедливы выражения (2,2*) и (3, 3*). В отличии от сферы внутри шара есть заряды, а значит напряженность поля отлична от нуля и потенциал не постоянен (рис.3). ![]() , где объемная плотность заряда шара постоянна и равна
, где объемная плотность заряда шара постоянна и равна 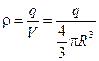 , напряженность поля внутри шара
, напряженность поля внутри шара ![]() (4), а потенциал
(4), а потенциал ![]() (5).
(5).
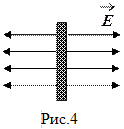 Бесконечная плоскость, равномерно заряженная с поверхностной плотностью заряда
Бесконечная плоскость, равномерно заряженная с поверхностной плотностью заряда ![]() , создает поле напряженностью
, создает поле напряженностью ![]() (6).
(6).
Разность потенциалов между двумя точками, находящимися на расстоянии х1
и х2 от плоскости, равна ![]()
![]() (7)
(7)
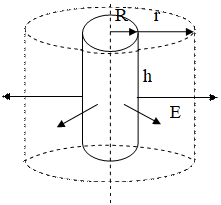 3) Бесконечный заряженный цилиндр радиуса R, заряженный с линейной плотностью
3) Бесконечный заряженный цилиндр радиуса R, заряженный с линейной плотностью ![]() , создает вокруг себя поле, силовые линии которого перпендикулярны поверхности цилиндра. Выберем в качестве гауссовой поверхности цилиндр радиусом r>R и высотой h. Заряд цилиндра, создающий поле, силовые линии которого пересекают гауссову поверхность, равен
, создает вокруг себя поле, силовые линии которого перпендикулярны поверхности цилиндра. Выберем в качестве гауссовой поверхности цилиндр радиусом r>R и высотой h. Заряд цилиндра, создающий поле, силовые линии которого пересекают гауссову поверхность, равен ![]() . По теореме Гаусса найдем напряженность поля на расстоянии r от центра цилиндра
. По теореме Гаусса найдем напряженность поля на расстоянии r от центра цилиндра ![]() , тогда
, тогда ![]() , связи напряженности и напряжения между двумя точками
, связи напряженности и напряжения между двумя точками 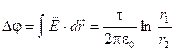
Поможем написать любую работу на аналогичную тему

