1. Пусть источник света S0 испускает сферическую волну. Поставим на пути волны непрозрачный экран Э1 с круглым отверстием АВ таким образом, чтобы перпендикуляр, опущенный из S0 на экран, проходил через центр отверстия (рис. 3.4 а). Для наблюдения дифракционной картины параллельно Э1 на расстоянии L от него поместим экран Э2. Используя метод зон Френеля, разобьем открытую часть волнового фронта АВ на зоны и определим результирующую амплитуду светового вектора в точке Р. Число открытых зон Френеля m зависит от размеров отверстия АВ, расстояния L и длины волны света λ. Если m – нечетное число, суммарная амплитуда в точке Р будет равна Е1/2 + Еm/2, что соответствует интерференционному максимуму На рис. 3.4 б показано, как меняется интенсивность света на экране Э2 в зависимости от расстояния r от центра экрана P. Следовательно, наличие преграды с круглым отверстием усиливает освещенность в точке Р, т.к. без экрана амплитуда в данной точке была бы равна Е1/2. Если m – четное число, результирующая амплитуда в точке Р:
.
Поскольку амплитуды двух соседних зон Френеля мало отличаются друг от друга, можно предположить, что 
и тогда результирующая амплитуда запишется в виде: 
и в точке Р будет наблюдаться интерференционный минимум (рис. 3.4 в). Чтобы найти результирующую амплитуду в другой точке экрана, например, Р’, необходимо разбить фронт волны на зоны с центром в точке О’ (рис. 3.4. а). В этом случае часть первоначальных зон будет закрыта экраном Э1. Амплитуда в точке 
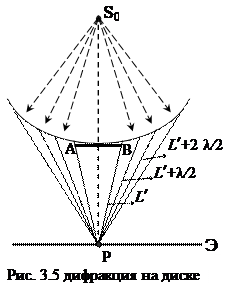Р’ будет определяться не только числом зон, укладывающихся на отверстии, но и степенью частичного перекрывания зон. Исходя из соображений симметрии, дифракционная картина должна состоять из чередующихся светлых и темных колец, что и было подтверждено экспериментально. По мере удаления от центра экрана интенсивность максимумов убывает. Если S0
– источник белого света, светлые кольца имеют радужную окраску.
2. Пусть между источником света S0 и экраном Э размещен непрозрачный диск АВ, параллельный экрану (рис. 3.5). Пунктирная прямая S0Р перпендикулярна диску и проходит через его центр. Вновь воспользуемся методом зон Френеля. Пусть диск закрывает m зон, тогда амплитуда первой действующей зоны будет Еm+1. С нее и следует начинать построение зон. В результате суммирования амплитуд всех открытых зон мы получаем, что в точке Р амплитуда Е = Еm+1/2. Таким образом, при дифракции на круглом непрозрачном диске в центре экрана получается светлое пятно (т.к. интенсивность здесь отлична от нуля), окруженное чередующимися концентрическими кольцами минимумов и максимумов.
Поможем написать любую работу на аналогичную тему